Versuchsplanung

Die statistische Versuchsplanung (englisch design of experiments, DOE) wird bei Entwicklung und Optimierung von Produkten oder Prozessen eingesetzt.

Da Versuche Ressourcen benötigen (Personal, Zeit, Geräte usw.), sieht sich der Versuchsverantwortliche in einem Zwiespalt zwischen einerseits der Genauigkeit und Zuverlässigkeit seiner erwarteten Ergebnisse und andererseits dem dazu notwendigen Aufwand. Der Begriff "Versuch" schließt neben materiellen Versuchen auch Rechnersimulationen mit ein.

Mit der statistischen Versuchsplanung wird mit möglichst wenigen Versuchen (Einzelexperimenten) der Wirkzusammenhang zwischen Einflussfaktoren (=unabhängige Variablen) und Zielgrößen (=abhängige Variable) möglichst genau ermittelt.

Versuchspläne

Im Gegensatz zur "althergebrachten" Vorgehensweise, bei der in einer Versuchsreihe jeweils nur ein Faktor variiert wird, werden bei der statistischen Versuchsplanung mehrere Faktoren gleichzeitig verändert.

Es werden sogenannte Versuchspläne erstellt, die Folgendes berücksichtigen:

• Anzahl der zu untersuchenden Faktoren (mind. 2)
• Art der zu untersuchenden Faktoren (nominal (=qualitativ) oder quantitativ)
• Bestehende Informationen
• Gewünschte Genauigkeit/Zuverlässigkeit der Aussagen

Klassische Pläne in der Versuchsplanung sind vollständige Versuchspläne, Teilfaktorpläne (sogenannte Screening-Pläne) und Response-Surface-Pläne.

Mit Screening-Plänen kann mit relativ wenigen Versuchen der Einfluss vieler Faktoren gleichzeitig untersucht werden, um so zu erkennen, welche wichtig sind.

Mit Response-Surface-Plänen kann der Zusammenhang zwischen den wenigen wichtigen Faktoren und den Zielgrößen dann im Detail untersucht werden, um optimale Einstellungen der Faktoren zu ermitteln.

Auswertung

Bei nominalen (kategorischen, qualitativen) Faktoren erfolgt die Auswertung mit Hilfe der Varianzanalyse. Bei quantitativen (metrischen) Faktoren erfolgt die Auswertung mit Hilfe der Regressionsanalyse. Am häufigsten werden Regressionsmodelle verwendet, die auf einer Linearkombination von Basisfunktionen beruhen:

• Lineares Modell ohne Wechselwirkungen (y = a₀ + a₁x₁ + a₂x₂ + a₃x₃ bei drei Faktoren)
• Lineares Modell mit Wechselwirkungen (y = a₀ + a₁x₁ + a₂x₂ + a₃x₃ + a₄x₁x₂ + a₅x₁x₃ + a₆x₂x₃ bei drei Faktoren)
• Quadratische (selten kubische) Modelle mit Wechselwirkungen (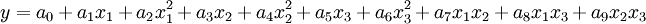$y=a_0 + a_1x_1 + a_2x_1^2+ a_3x_2 + a_4x_2^2 + a_5x_3 + a_6x_3^2 + a_7 x_1x_2 + a_8 x_1x_3 + a_9 x_2x_3$ bei drei Faktoren)

Diese Modelle kann man als Taylor-Entwicklungen bis zum Grad n = 1 bzw. n = 2 auffassen. Die Modellparameter a_i werden so bestimmt, dass die Abweichungen zwischen Daten und Modell möglichst klein sind (meist wird die Summe der quadrierten Abweichungen minimiert).

Kennt man die tatsächliche Form des funktionalen Zusammenhangs zwischen Faktoren und Zielgrößen, so kann man die Parameter in dieser Funktion mit nichtlinearer Regression anpassen.

Software zur statistischen Versuchsplanung

Viele der großen kommerziellen Statistikpakete besitzen auch ein Modul zur statistischen Versuchsplanung. Es gibt allerdings auch spezielle Software, die dem statistisch nicht so versierten Benutzer die Durchführung der Planung und der Auswertung erleichtert. Dies geschieht natürlich auf Kosten der Flexibilität. Möglich ist dies beispielsweise mit Design Expert, Minitab oder STATISTICA.

Daneben enthalten verschiedenartige Simulationspakete oft speziell zugeschnitte Programme oder Module zur statistischen Versuchsplanung.

Literatur

Englische Standardwerke (Auswahl)

• George E. P. Box, J. Stuart Hunter, William G. Hunter: Statistics for Experimenters: Design, Innovation, and Discovery. 2. Auflage. Wiley & Sons, 2005, ISBN 0471718130. 
• A. Dean, Angela Dean, D. Voss: Design and Analysis of Experiments. 2. Auflage. Springer, Berlin, 2003, ISBN 0387985611. 
• Raymond H. Myers, Douglas C. Montgomery: Response Surface Methodology: Process and Product Optimization Using Designed Experiments. 2. Auflage. Wiley & Sons, 2002, ISBN 0471412554. 
• Douglas C. Montgomery: Design and Analysis of Experiments. 6. Auflage. Wiley & Sons, 2005, ISBN 047148735X. 

Deutsche Einführung (Auswahl)

• W. Kleppmann: Taschenbuch Versuchsplanung - Produkte und Prozesse optimieren, Hanser, 5. Auflage 2008. ISBN 978-3-446-41595-9
• Bernd Klein: Versuchsplanung - DoE - Einführung in die Taguchi/Shainin-Methodik, Oldenbourg, 2007. ISBN 978-3-486-58352-6
• Wilker, Holger: Systemoptimierung in der Praxis, Teil 1 - Leitfaden zur statistischen Versuchsauswertung, Norderstedt 2006.ISBN 978-3-833-44551-4
• Wilker, Holger: Systemoptimierung in der Praxis, Teil 2 - Leitfaden zur statistischen Versuchsplanung, Norderstedt 2006.ISBN 978-3-833-46306-8
• H. Bandemer, A. Bellmann: Statistische Versuchsplanung 4. Auflage 1994 ISBN 3-8154-2079-2
• H. Bandemer u.a.: Theorie und Anwendung der optimalen Versuchsplanung Bd. I Akademie - Verlag Berlin 1974
• H. Bandemer, W. Näther: Theorie und Anwendung der optimalen Versuchsplanung Bd. II Akademie - Verlag Berlin 1974
• K. Hartmann, E. Letzki, W. Schäfer: Statistische Versuchsplanung und -auswertung in der Stoffwirtschaft Verlag für Grundstoffindustrie 1974
• H. Petersen: Grundlagen der Statistik und der statistischen Versuchsplanung Bd. I-II ecomed 1991
• E. Scheffler: Einführung in die Praxsis der statistischen Versuchsplanung" Deutscher Verlag für Grundstoffindustrie 1984
• V. Nollau: Statistische Analysen Birkhäuser Verlag 1978
• D. Rasch, G. Herrendörfer, J. Bock, K. Busch: Versuchsplanung und Auswertung - Verfahrensbibliothek Bd. I-III Deutscher Landwirtschaftsverlag Berlin 1978
• D. Rasch: Statistische Versuchsplanung G. Fischer Verlag Stuttgart 1992

Weblinks

• Methoden zur Zuverlässigkeitsermittlung