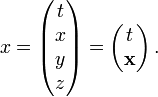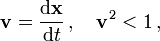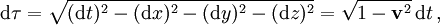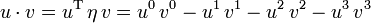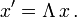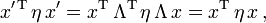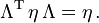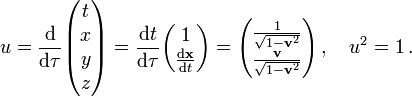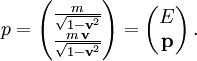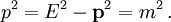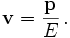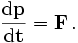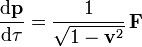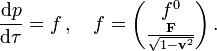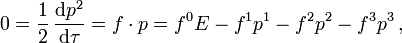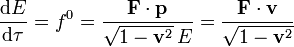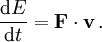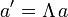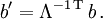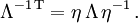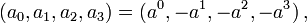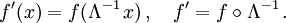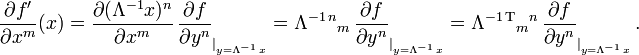Viererkraft

Ein Vierervektor ist ein Vektor in einem reellen, vierdimensionalen Raum mit einem indefiniten Längenquadrat. In zwei gegeneinander bewegten Inertialsystemen hängen die Komponenten des Vierervektors durch eine Lorentztransformation miteinander zusammen. Beispielsweise sind die Zeit- und Ortskoordinaten eines Ereignisses in der Raumzeit die Komponenten eines Vierervektors, ebenso sind die Energie und der Impuls eines Teilchens die Komponenten eines Vierervektors.

Ortsvektor

Bei Ereignissen ist wie bei Verabredungen wichtig, wann und wo sie stattfinden. Diese Angaben fasst der Orts-Vierervektor oder kürzer Ortsvektor in einem Spaltenvektor zusammen, den wir aber im laufenden Text des Druckbildes wegen als Zeile x = (x⁰,x¹,x²,x³) schreiben. Die oben stehenden Zahlen bedeuten hier keinen Exponenten, sondern zählen die Komponenten ab.

Die Nullkomponente des Ortsvektors ist die mit der Lichtgeschwindigkeit multiplizierte Zeit, 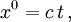$x^0=c\,t\,,$ zu der das Ereignis stattfindet, die nächsten drei Komponenten, 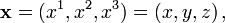$\mathbf x = (x^1,x^2,x^3)=(x,y,z)\,,$ bezeichnen den Ort.

Genauer sind dies die kartesischen Koordinaten, mit denen ein gleichförmig bewegter Beobachter, der sich nicht dreht, angibt, wann und wo das Ereignis stattfindet. Aus dem Zusammenhang erschließt man, ob x für den Vierervektor oder seine erste räumliche Komponente steht.

Wir verwenden als Längeneinheit die Strecke, die Licht in einer Sekunde zurücklegt und nennen sie eine Sekunde. Dann ist die Lichtgeschwindigkeit dimensionslos und hat den Wert c = 1. In solchen Maßsystemen ist der Vektor, der ein Ereignis bezeichnet,

$x= \begin{pmatrix}t\\x\\y\\z\end{pmatrix}= \begin{pmatrix}t\\\mathbf x \end{pmatrix}\,.$

Die Menge aller Ereignisse ist die Raumzeit. Das Längenquadrat

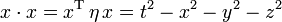$x\cdot x = x^{\text{T}}\,\eta \,x = t^2 - x^2- y^2 - z^2$ mit $\eta=\mathrm{diag}\left( 1,-1,-1,-1,\right)$

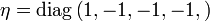
ist wegen des folgenden physikalischen Sachverhalts wichtig:

Auf einer mit Geschwindigkeit

$\mathbf v= \frac{\mathrm d \mathbf x}{\mathrm d t}\,,\quad \mathbf v^2 < 1\,,$

bewegten Uhr, die das Ereignis (t,x,y,z) durchläuft, vergeht die Zeit

$\mathrm d \tau = \sqrt{(\mathrm d t)^2 - (\mathrm d x)^2- (\mathrm d y)^2 - (\mathrm d z)^2}=\sqrt{1-\mathbf v^2}\,\mathrm d t\,,$

bis sie das benachbarte Ereignis (t + dt,x + dx,y + dy,z + dz) durchläuft.

Diese zeitliche Entfernung, die Eigenzeit, ist in der relativistischen Physik für das Messen von Zeiten und Längen ebenso wichtig wie in Euklidischer Geometrie die Länge von Strecken.

Daher nennt man die quadratische Form, die das Längenquadrat definiert, auch wenn sie nicht positiv definit ist, die Metrik der Raumzeit. Die Bilinearform

$u\cdot v = u^{\text{T}}\,\eta \,v = u^0\,v^0 - u^1\,v^1- u^2\,v^2- u^3\,v^3$

heißt das Skalarprodukt der Vierervektoren u und $v\,.$

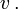
Bei Lorentztransformationen ändern sich die Komponenten des Ortsvektors in

$x^\prime =\Lambda\, x\,.$

Dabei bleibt das Längenquadrat ungeändert

$x^{\prime\,\text{T}}\,\eta\,x^\prime =x^{\text{T}}\,\Lambda^{\text{T}}\,\eta\,\Lambda\, x= x^{\text{T}}\,\eta\,x\,,$

denn Lorentztransformationen erfüllen definitionsgemäß

$\Lambda^{\text{T}}\,\eta\,\Lambda = \eta\,.$

Vierervektoren, deren Zeitkomponente überwiegt, 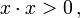$x\cdot x > 0\,,$ nennt man zeitartig, überwiegen die räumlichen Komponenten, 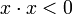$x\cdot x < 0$, so heißt x raumartig, ist der räumliche Teil so groß wie der zeitliche, 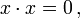$x\cdot x = 0\,,$ so heißt x lichtartig.

Ist bei zwei Ereignissen a und b die Differenz b − a zeitartig oder lichtartig und ist b⁰ > a⁰, dann kann b die Auswirkung von a sein. Falls b − a raumartig ist, kann es sich bei a und b nicht um Ursache und Auswirkung handeln.

Vierergeschwindigkeit

Die Vierergeschwindigkeit (u⁰,u¹,u²,u³) eines Teilchens, das eine Weltlinie 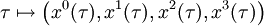$\tau \mapsto \bigl(x^0(\tau),x^1(\tau),x^2(\tau),x^3(\tau)\bigr)$ durchläuft, ergibt sich durch Ableiten nach der Eigenzeit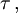 $\tau\,,$

$u =\frac{\mathrm d}{\mathrm d\tau } \begin{pmatrix} t\\x\\y\\z \end{pmatrix} = \frac{\mathrm d t}{\mathrm d \tau } \begin{pmatrix} 1\\ \frac{\mathrm d \mathbf x}{\mathrm d t }\\ \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{1-\mathbf v^2}} \\ \frac{\mathbf v}{\sqrt{1-\mathbf v^2}} \end{pmatrix}\,,\quad u^2=1\,.$

Die Vierergeschwindigkeit ist der auf Einheitslänge normierte Tangentialvektor an die Weltlinie des Teilchens.

Viererimpuls

Die Vierergeschwindigkeit eines Teilchens, mit seiner Masse m multipliziert, ergibt den Viererimpuls

$p = \begin{pmatrix} \frac{m}{\sqrt{1-\mathbf v^2}}\\ \frac{m\,\mathbf v}{\sqrt{1-\mathbf v^2}} \end{pmatrix}= \begin{pmatrix} E \\ \mathbf p \end{pmatrix}\,.$

Seine Nullkomponente ist die Energie E, seine räumlichen Komponenten sind die Komponenten der Impulses 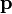$\mathbf p$ des relativistischen Teilchens. Unabhängig von der Geschwindigkeit hängen Energie und Impuls durch die Energie-Impuls-Beziehung mit der Masse zusammen,

$p^2= E^2 - \mathbf{p}^2 = m^2\,.$

Das Verhältnis von Impuls zu Energie ist die Geschwindigkeit

$\mathbf v= \frac{\mathbf p}{E}\,.$

Viererkraft

Die Bewegungsgleichung besagt, dass sich der Impuls des Teilchens mit der Zeit um den übertragenen Impuls ändert. Der pro Zeit übertragene Impuls ist die Kraft $\mathbf F\,,$

$\mathbf \frac{\mathrm d\mathbf p}{\mathrm d t}=\mathbf F\,.$

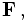
Für die Ableitung nach der Eigenzeit besagt dies

$\frac{\mathrm d\mathbf p}{\mathrm d \tau}= \frac{1}{\sqrt{1-\mathbf v^2}}\, \mathbf F$

und für den Viererimpuls

$\frac{\mathrm d p}{\mathrm d \tau}= f \,,\quad f = \begin{pmatrix} f^0\\ \frac{\mathbf F}{\sqrt{1-\mathbf v^2}} \end{pmatrix}\,.$

Die hierbei auftretende Viererkraft f hat nicht vier frei vorgebbare Komponenten. Da stets die Energie-Impuls-Beziehung p² = m² gelten muss, steht die Viererkraft senkrecht auf dem Viererimpuls

$0 = \frac 1 2 \,\frac{\mathrm d p^2}{\mathrm d \tau}= f\cdot p = f^0 E - f^1 p^1- f^2 p^2- f^3 p^3\,,$

das heißt, die pro Eigenzeit übertragene Energie muss mit der Kraft und dem Impuls durch

$\frac{\mathrm d E}{\mathrm d \tau}=f^0 = \frac{\mathbf F\cdot\mathbf p}{\sqrt{1-\mathbf v^2}\,E}= \frac{\mathbf F\cdot\mathbf v}{\sqrt{1-\mathbf v^2}}$

zusammenhängen. (Je nach Zusammenhang bezeichnet der Punkt das Skalarprodukt von Vierer- oder Dreiervektoren.) Die pro Zeit übertragene Energie ist gleich der pro Zeit verrichteten Arbeit

$\frac{\mathrm d E}{\mathrm d t} = \mathbf F\cdot\mathbf v\,.$

Ko- und kontravariante Vektoren

Die Komponenten eines kontravarianten Vierervektors a gehen bei Lorentztransformationen Λ in

$a^\prime =\Lambda\, a$

über. Man schreibt seine Komponenten a = (a⁰,a¹,a²,a³) mit oben stehenden Zahlen.

Unten stehende Indizes b = (b₀,b₁,b₂,b₃) kennzeichnen Komponenten eines kovarianten Vierervektors mit dem kontragredienten (entgegengesetzten) Transformationsgesetz

$b^\prime =\Lambda^{-1\,\text{T}}\,b\,.$

Die beiden Transformationsgesetze sind nicht gleich, aber äquivalent, denn Lorentztransformationen erfüllen definitionsgemäß

$\Lambda^{-1\,\text{T}}=\eta\,\Lambda\,\eta^{-1}\,.$

Daher ergibt 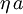$\eta\,a$ die Komponenten des kovarianten Vektors,

$(a_0,a_1,a_2,a_3)=(a^{0},-a^{1},-a^{2},-a^{3})\,,$

der dem kontravarianten Vektor a = (a⁰,a¹,a²,a³) zugeordnet ist.

Beispielsweise sind die partiellen Ableitungen einer Funktion f(x) die Komponenten eines kovarianten Vektors. Lorentztransformationen bilden x auf 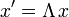$x^\prime = \Lambda \,x$ ab und definieren die transformierte Funktion 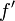$f^\prime$ durch die Forderung 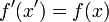$f^\prime(x^\prime)=f(x)$, dass die transformierte Funktion am transformierten Ort denselben Wert habe, wie die ursprüngliche Funktion am ursprünglichen Ort

$f^\prime(x)=f(\Lambda^{-1}\,x)\,,\quad f^\prime = f\circ \Lambda^{-1}\,.$

Die partiellen Ableitungen transformieren wegen der Kettenregel kontragredient,

$\frac{\partial f^\prime}{\partial x^m}(x)= \frac{\partial (\Lambda^{-1}x)^n}{\partial x^m}\, \frac{\partial f}{\partial y^n}_{|_{y=\Lambda^{-1}\,x}}= \Lambda^{-1\,n}{}_m\, \frac{\partial f}{\partial y^n}_{|_{y=\Lambda^{-1}\,x}}= \Lambda^{-1 \,\text{T}}{}_m{}^n\, \frac{\partial f}{\partial y^n}_{|_{y=\Lambda^{-1}\,x}}\,.$

Literatur

• L. D. Landau, E. M. Lifschitz: Lehrbuch der Theoretischen Physik - Band 2 - Klassische Feldtheorie. Verlag Harri Deutsch, 1997.
• T. Fließbach: Allgemeine Relativitätstheorie. BI Wissenschaftsverlag, 1990. (mit einem Kapitel über Spezielle Relativitätstheorie)
• Walter Greiner, Johann Rafelski: Spezielle Relativitätstheorie. Verlag Harri Deutsch, 1989.

Weblinks

• Norbert Dragon Geometrie der Relativitätstheorie