Viererlemma

Das Fünferlemma ist ein in der Mathematik, hauptsächlich in der homologischen Algebra und anderen Anwendungen abelscher Kategorien, häufig verwendetes und wichtiges Lemma über kommutative Diagramme. Das Fünferlemma ist nicht nur für abelsche Kategorien gültig, sondern auch beispielsweise für die Kategorie der Gruppen.

Das Fünferlemma kann gedacht werden als die Kombination zweier anderer zueinander dualer Aussagen, nämlich der Viererlemmata.

Aussagen

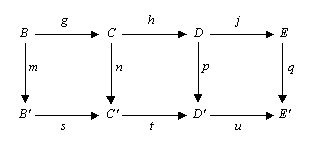
Man betrachte das folgende kommutative Diagramm in einer beliebigen abelschen Kategorie (etwa der Kategorie der Vektorräume über einem gegebenen Körper) oder der Kategorie der Gruppen:

Die Zeilen seien exakt, m und p seien Isomorphismen, l ein Epimorphismus, q ein Monomorphismus. Das Fünferlemma besagt, dass dann n ebenfalls ein Isomorphismus ist.

Das (erste) Viererlemma besagt: Sind in dem kommutativen Diagramm

die Zeilen exakt, m und p Epimorphismen und q ein Monomorphismus, so ist n ein Epimorphimus.

Das (zweite) Viererlemma besagt: Sind in dem kommutativen Diagramm

die Zeilen exakt, m und p Monomorphismen und l ein Epimorphismus, so ist n ein Monomorphimus.

Beweis

Der Beweis erfolgt durch Diagrammjagd, im Folgenden ausgeführt in der Kategorie der Gruppen (das neutrale Element wird jeweils durch 1 bezeichnet, die Verknüpfung als Multiplikation geschrieben). Er ist (in additive Schreibweise übersetzt) direkt übertragbar auf die Kategorie der abelschen Gruppen oder der Moduln über einem Ring und gilt somit nach dem Einbettungssatz von Mitchell in allen abelschen Kategorien.

Für den Beweis des ersten Viererlemmas seien also in

die Zeilen exakt, m und p surjektiv und q injektiv. Zu zeigen ist, dass n surjektiv ist.

Sei also c' ein beliebiges Element von C'.

Da p surjektiv ist, gibt es ein d in D mit p(d)=t(c').

Wegen der Kommutativität des Diagramms ist q(j(d))=u(p(d)).

Wegen der Exaktheit ist u(t(c'))=1, also q(j(d))=1.

Wegen der Injektivität von q folgt hieraus j(d)=1.

Da d im Kern von j liegt, liegt es im Bild von h, d.h. es gibt ein c aus C mit h(c)=d.

Dann gilt t(n(c)) = p(h(c)) = p(d) = t(c').

Folglich gilt c' = x ·n(c) für ein x aus ker t = im s.

Sei also b' ein Element von B' mit s(b')=x.

Da m surjektiv ist, gibt es ein b in B mit m(b)=b'.

Es folgt n(g(b)·c) = n(g(b))·n(c) = s(m(b))·n(c) = s(b'))·n(c) = x ·n(c) = c'.

Somit ist n in der Tat surjektiv.

Das zweite Viererlemma ist dual zum ersten bzw. kann auf dieselbe einfache Weise bewiesen werden.

Das Fünferlemma folgt dann unmittelbar durch Kombination der beiden Viererlemmata.

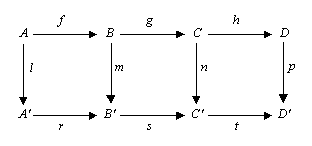
Kurzes Fünferlemma

Sind in dem kommutierenden Diagramm

die Zeilen kurze exakte Sequenzen und g und h Isomorphismen, so ist auch f ein Isomorphismus.

Dies folgt sofort (wiederum für abelsche Kategorien oder die Kategorie der Gruppen) aus dem Fünferlemma, da man die Nullabbildung zwischen den Nullobjekten ergänzen kann.

Gerade beim kurzen Fünferlemma besteht ein häufiger Irrtum darin, auf die Isomorphie von B und B' zu schließen, sobald man Isomorphismen g und h findet. Dies ist jedoch ein Trugschluss, denn das Lemma behauptet nicht die Existenz eines Isomorphismus, solange man nicht wenigstens überhaupt einen zu g und h passenden Homomorphismus f hat.

Anwendungen

Das Fünferlemma wird häufig auf lange exakte Sequenzen angewendet: Um die Homologie oder Kohomologie eines gegebenen Objektes zu berechnen, verwendet man typischerweise ein einfacheres Unterobjekt mit bekannter (Ko-)Homologie. Dies liefert eine lange exakte Sequenz, in der die gesuchten Homologie-Gruppen auftauchen. Dies allein reicht zwar normalerweise nicht, um die Homologie-Gruppen zu bestimmen; kann man aber das ursprüngliche Objekt samt Unterobjekt über Morphismen mit bekannten Objekten vergleichen, so wird ein Homomorphismus zwischen langen exakten Sequenzen induziert und das Fünferlemma kann dann die unbekannten Gruppen bestimmen.

Siehe auch

• Schlangenlemma, ein weiterer durch Diagrammjagd bewiesener Satz.
• Neunerlemma

Weblinks

• Margherita Barile: Five Lemma auf MathWorld (englisch)