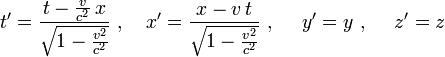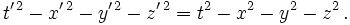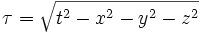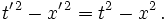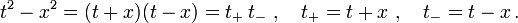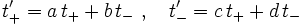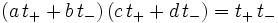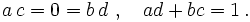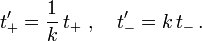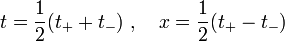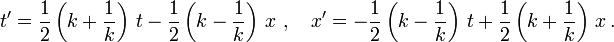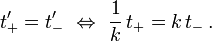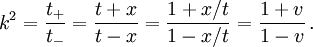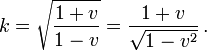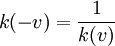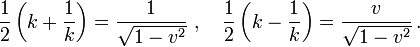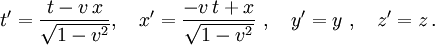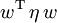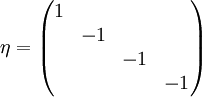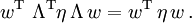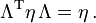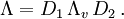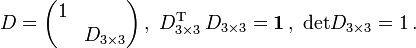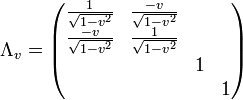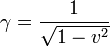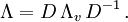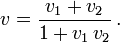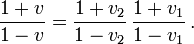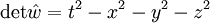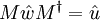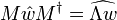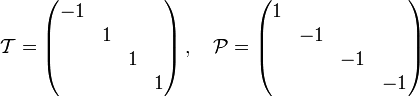- Lorentztransformation
-
Die Lorentz-Transformationen verbinden in der speziellen Relativitätstheorie und der lorentzschen Äthertheorie die Zeit- und Ortskoordinaten, mit denen verschiedene Beobachter angeben, wann und wo Ereignisse stattfinden.
Dabei handelt es sich um gradlinig gleichförmig bewegte Beobachter, deren Relativgeschwindigkeit kleiner als die Lichtgeschwindigkeit ist, und um Koordinaten, in denen kräftefreie Teilchen gerade Weltlinien durchlaufen. Bei Lorentz-Transformationen bleibt die Lichtgeschwindigkeit c unverändert.
Ist ein gleichförmig bewegter Beobachter mit Geschwindigkeit v in x-Richtung gegenüber einem anderen Beobachter bewegt, so hängen die Koordinaten
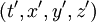 , die er einem Ereignis zuschreibt, durch die Lorentz-Transformation
, die er einem Ereignis zuschreibt, durch die Lorentz-Transformationmit den Koordinaten (t,x,y,z) zusammen, die der andere Beobachter für dasselbe Ereignis verwendet.
Inhaltsverzeichnis
Geschichtliche Entwicklung
Die Arbeiten von Woldemar Voigt (1887), Hendrik Antoon Lorentz (1895, 1899, 1904), Joseph Larmor (1897, 1900) und Henri Poincaré (1905, welcher den Lorentztransformationen ihren Namen gab) zeigten, dass die Lösungen der Gleichungen der Elektrodynamik durch Lorentztransformationen aufeinander abgebildet werden oder mit anderen Worten, dass die Lorentz-Transformationen Symmetrien der Maxwell-Gleichungen sind.
Man versuchte damals, die elektromagnetischen Phänomene durch einen hypothetischen Äther zu erklären. Als bemerkenswerteste Eigenschaft dieses Äthers stellte sich allerdings heraus, dass sich von ihm keine Spur nachweisen ließ. In seiner Äthertheorie konnte Lorentz dies dadurch erklären, dass die Längenmaßstäbe sich bei Bewegung in Bewegungsrichtung verkürzen und dass bewegte Uhren eine langsamer verlaufende Zeit, die er Ortszeit nannte, anzeigen. Die von Lorentz angegebenen Transformationen der Längen und Zeiten, die bewegte Uhren und Maßstäbe anzeigen, bildeten eine Gruppe und waren damit mathematisch stimmig. Auch wenn in Lorentz' Äthertheorie eine gleichförmige Bewegung gegenüber dem Äther nicht nachweisbar war, hielt Lorentz an der Vorstellung eines Äthers fest, der ein absolut ruhendes, aber eben nicht nachweisbares, System auszeichnete.
Einsteins spezielle Relativitätstheorie löste Newtons Mechanik und die Ätherhypothese ab. Er leitete seine Theorie aus dem Relativitätsprinzip ab, dass sich im Vakuum unter Vernachlässigung von gravitativen Effekten Ruhe nicht von gleichförmiger Bewegung unterscheiden lässt. Insbesondere hat Licht im Vakuum für jeden Beobachter dieselbe Geschwindigkeit c. Die Zeit- und Ortskoordinaten, mit denen zwei gleichförmig bewegte Beobachter Ereignisse bezeichnen, hängen dann durch eine Lorentz-Transformation miteinander zusammen, statt wie in Newtons Mechanik durch eine Galilei-Transformation.
- Hauptartikel: Geschichte der Lorentz-Transformation
Herleitung
Die folgenden Überlegungen klären, wie Koordinaten zusammenhängen, die gleichförmig bewegte Beobachter zur Benennung der Zeit und des Ortes von Ereignissen verwenden.
Um das Formelbild einfach zu halten, verwenden wir als Längeneinheit die Strecke, die Licht in einer Sekunde zurückgelegt und nennen sie eine Sekunde. Dann haben Zeit und Länge dieselbe Maßeinheit und die dimensionslose Lichtgeschwindigkeit beträgt
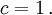 Untersuchungen in anderen Maßsystemen bringen keine tieferen Einsichten.
Untersuchungen in anderen Maßsystemen bringen keine tieferen Einsichten.Für alle gleichförmig bewegten Beobachter durchlaufen freie Teilchen gerade Weltlinien. Daher muss die Transformation Geraden auf Geraden abbilden. Mathematisch besagt dies, dass die Transformation linear inhomogen ist.
Stimmen beide Beobachter in der Wahl des Zeitnullpunkts und des räumlichen Ursprungs überein, dann ist die gesuchte Transformation linear und homogen.
Zudem muss die Differenz t2 − x2 − y2 − z2 bei beiden Beobachtern übereinstimmen
Denn auf einer gleichförmig bewegten Uhr, die den Ursprung durchläuft, vergeht die Zeit
bis sie das Ereignis durchläuft, das der eine Beobachter mit (t,x,y,z) und der andere mit
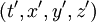 benennt. Da beide Beobachter diese Uhr ablesen können und darin übereinstimmen, welchen Wert sie in einem Ereignis anzeigt, müssen die obigen Differenzen von Quadraten übereinstimmen.
benennt. Da beide Beobachter diese Uhr ablesen können und darin übereinstimmen, welchen Wert sie in einem Ereignis anzeigt, müssen die obigen Differenzen von Quadraten übereinstimmen.Unterstellen wir einfachheitshalber, dass die y- und z-Koordinaten beider Beobachter übereinstimmen, dann suchen wir eine lineare Transformation von (t,x) auf
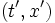 mit
mitDie Aufgabe vereinfacht sich durch Verwendung der Binomialformel
Es ist also eine lineare Transformation
mit Koeffizienten a,b,c,d gesucht, so dass
gilt. Ausmultiplizieren und Vergleich der Koeffizienten ergibt
Eine Lösung ist b = c = 0, wobei
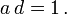 Diese lineare Transformation staucht t + um denselben Faktor, um den sie t − streckt,
Diese lineare Transformation staucht t + um denselben Faktor, um den sie t − streckt,Für die Zeit- und Raumkoordinaten
besagt dies
Die Bedeutung des Parameters k wird klar, wenn wir bedenken, dass auf der Weltlinie des bewegten Beobachters
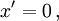 also
also 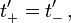 gilt: jeder Beobachter ruht im Ursprung seines Bezugssystems. In den Koordinaten des ruhenden Beobachters gilt für die Weltlinie des bewegten Beobachters
gilt: jeder Beobachter ruht im Ursprung seines Bezugssystems. In den Koordinaten des ruhenden Beobachters gilt für die Weltlinie des bewegten BeobachtersLösen wir nach k auf, setzen t + und t − ein, kürzen und bedenken, dass v = x / t die Geschwindigkeit des bewegten Beobachters ist, so erhalten wir
Ziehen wir die Wurzel (die negative Wurzel würde zu einem Beobachter gehören, dessen Zeit rückwärts liefe) und erweitern wir mit
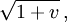 so ergibt sich
so ergibt sichIn dieser Form ist klar, dass der inverse Streckungsfaktor zur umgekehrten Geschwindigkeit gehört
und
Setzen wir dies ein, so erhalten wir die in der Einleitung angegebene Lorentztransformation
Dabei sind die gestrichenen Koordinaten diejenigen, die ein in x-Richtung mit Geschwindigkeit v bewegter Beobachter für ein Ereignis verwendet, und die ungestrichenen Koordinaten diejenigen, mit denen ein ruhender Beobachter dasselbe Ereignis bezeichnet.
Gruppeneigenschaften
Die Lorentz-Transformation beschreibt den Übergang von einem Inertialsystems K zu einem anderen Inertialsystem K', der den Abstand zweier Vierervektoren invariant lässt:
Die allgemeine Transformationsgleichung ist
Die Lorentz-Transformation lässt sich danach klassifizieren, ob Raum-Zeit-Translationen aμ auftreten. Die Menge aller Transformationen bilden eine Gruppe:
 : inhomogene Lorentz-Gruppe bzw. Poincaré-Gruppe
: inhomogene Lorentz-Gruppe bzw. Poincaré-Gruppe
- aμ = 0: homogene Lorentz-Gruppe (oft einfach "Lorentz-Gruppe", siehe Spezielle Lorentztransformation)
- hier ist neben dem Abstand auch das Skalarprodukt zweier Vierervektoren unter Transformation invariant: xμyμ = x'μy'μ
- somit auch das Normquadrat (Längenquadrat) eines Vektors: xμxμ = x'μx'μ
Die homogene Lorentz-Gruppe lässt sich weiter spezialisieren in:
 : Homogene Transformationen
: Homogene Transformationen : Orthochrone Transformationen
: Orthochrone Transformationen : Eigentliche Transformationen
: Eigentliche Transformationen
Eigentliche Transformationen lassen sich mit 6 Parametern (drei Raumdrehwinkel und drei Boost-Winkel) beschreiben. Unter eigentlicher Transformation werden die Zeitrichtung und der Richtungssinn der drei Raumachsen nicht verändert.
Die eigentlichen Transformationen (6 Parameter) bilden zusammen mit den Raum-Zeit-Translationen (4 Parameter) die 10 parametrige "eigentliche orthochrone Poincaré-Gruppe".
Lorentzgruppe
- Hauptartikel: Lorentz-Gruppe
Lorentztransformationen bilden die Lorentzgruppe O(1,3), das ist die Gruppe der linearen Transformationen von
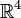 auf
auf 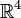 , die das Längenquadrat
, die das Längenquadrat- w2 = t2 − x2 − y2 − z2
jedes Vektors w = (t,x,y,z) aus
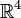 invariant lassen. Schreiben wir das Längenquadrat als Matrixprodukt
invariant lassen. Schreiben wir das Längenquadrat als Matrixproduktdes Spaltenvektors w (den wir im laufenden Text als Zeile notieren) mit der Matrix
und der transponierten Spalte, der Zeile wT, so muss für jeden Lorentztransformierten Vektor Λw gelten
Dies ist genau dann der Fall, wenn die Lorentztransformation die Gleichung
erfüllt.
Alle Lösungen dieser Gleichung, die die Zeitrichtung und räumliche Orientierung nicht umdrehen, sind von der Form
Dabei sind D1 und D2 Drehungen
Drehungen bilden die Untergruppe SO(3) der Lorentzgruppe. Die Matrix
bewirkt die oben angegebene Lorentztransformation mit einer Geschwindigkeit
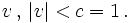
Der hier auftretende Faktor
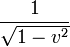 heißt Lorentzfaktor. Er wird häufig mit
heißt Lorentzfaktor. Er wird häufig mitabgekürzt.
Die Transformationen
heißen Lorentzboost. Sie transformieren auf die Koordinaten des bewegten Beobachters, der sich mit Geschwindigkeit v in die Richtung bewegt, die sich durch die Drehung D aus der x-Richtung ergibt.
Geschwindigkeitsaddition
- Hauptartikel: Relativistisches Additionstheorem für Geschwindigkeiten
Hintereinander ausgeführte Lorentzboosts in dieselbe Richtung mit Geschwindigkeit v1 und v2 ergeben Lorentzboosts mit der Gesamtgeschwindigkeit
Dies ergibt sich aus der Transformation (siehe oben)
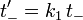 und
und 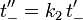 also
also 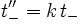 mit
mit 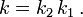
Setzen wir in
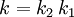 ein, wie die Faktoren k von der Geschwindigkeit abhängen, und quadrieren wir, so gilt
ein, wie die Faktoren k von der Geschwindigkeit abhängen, und quadrieren wir, so giltDies lässt sich leicht nach der Gesamtgeschwindigkeit v auflösen und ergibt, wie sich bei Bewegung in dieselbe Richtung Geschwindigkeiten kombinieren.
Hintereinander ausgeführte Lorentzboosts in verschiedene Richtungen ergeben normalerweise keine Lorentzboosts: die Menge der Lorentzboosts ist keine Untergruppe der Lorentztransformationen.
Überlagerungsgruppe
Die Matrix
ist hermitesch. Umgekehrt ist jede hermitesche
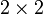 -Matrix von dieser Form, die hermiteschen
-Matrix von dieser Form, die hermiteschen 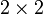 -Matrizen bilden einen vierdimensionalen, reellen Vektorraum.
-Matrizen bilden einen vierdimensionalen, reellen Vektorraum.Die Determinante
ist das Längenquadrat des Vierervektors
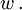
Multipliziert man
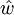 von links mit einer beliebigen, komplexen
von links mit einer beliebigen, komplexen 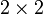 -Matrix und von rechts mit der hermitesch adjungierten, so ist das Ergebnis wieder hermitesch
-Matrix und von rechts mit der hermitesch adjungierten, so ist das Ergebnis wieder hermiteschund lässt sich als
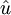 schreiben, wobei u = Λw linear von w abhängt. Ist M aus der speziellen linearen Gruppe der komplexen
schreiben, wobei u = Λw linear von w abhängt. Ist M aus der speziellen linearen Gruppe der komplexen 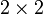 -Matrizen,
-Matrizen, 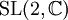 , deren Determinanten den speziellen Wert 1 haben, so stimmt das Längenquadrat von w und u = Λw überein, Λ ist also eine Lorentztransformation. Zu jedem M aus
, deren Determinanten den speziellen Wert 1 haben, so stimmt das Längenquadrat von w und u = Λw überein, Λ ist also eine Lorentztransformation. Zu jedem M aus 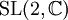 gehört vermöge
gehört vermögeeine Lorentztransformation Λ aus O(1,3).
Genauer gilt: Zu jedem Paar
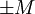 von komplexen
von komplexen 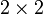 -Matrizen aus
-Matrizen aus 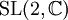 gehört genau eine Lorentztransformation Λ(M) = Λ( − M) aus dem Teil von O(1,3), der mit der
gehört genau eine Lorentztransformation Λ(M) = Λ( − M) aus dem Teil von O(1,3), der mit der 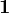 stetig zusammenhängt. Dieser Teil der Lorentzgruppe ist eine Darstellung der Gruppe
stetig zusammenhängt. Dieser Teil der Lorentzgruppe ist eine Darstellung der Gruppe 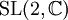
Die Gruppe
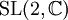 ist die Produktmannigfaltigkeit
ist die Produktmannigfaltigkeit 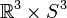 und einfach zusammenhängend. Der mit der
und einfach zusammenhängend. Der mit der 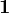 zusammenhängende Teil der Lorentzgruppe ist nicht einfach zusammenhängend.
zusammenhängende Teil der Lorentzgruppe ist nicht einfach zusammenhängend.Zeit- und Raumspiegelung
Die nicht mit der
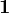 zusammenhängenden Lorentztransformationen erhält man, indem man die Zeitspiegelung oder die Raumspiegelung
zusammenhängenden Lorentztransformationen erhält man, indem man die Zeitspiegelung oder die Raumspiegelungoder beide mit den Lorentztransformationen multipliziert, die mit der
 zusammenhängen. Die Lorentzgruppe O(1,3) hat vier Zusammenhangskomponenten.
zusammenhängen. Die Lorentzgruppe O(1,3) hat vier Zusammenhangskomponenten.Referenzen
- Charles Kittel, Mechanik, Vieweg, Braunschweig 1973. (Berkeley Physik Kurs ; Band 1) ISBN 3-528-08351-4 Kap. 11, S.232
- Norbert Dragon, Geometrie der Relativitätstheorie
Siehe auch
Lorentz-Transformation und Minkowski-Raum
Weblinks
Wikimedia Foundation.