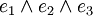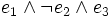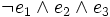- Vollkonjugat
-
Als Vollkonjunktion (auch: Minterm, Miniterm oder Elementarkonjunktion) bezeichnet man in der Aussagenlogik einen speziellen Konjunktionsterm, d. h. eine Anzahl von Buchstaben (Literalen), die alle durch ein logisches und (
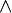 ) verknüpft sind. Dabei müssen alle n Variablen der betrachteten n-stelligen booleschen Funktion im Konjunktionsterm vorkommen, um von einer Vollkonjunktion sprechen zu können. Vollkonjunktionen lassen sich zu einer disjunktiven Normalform zusammensetzen, was unter anderem beim Verfahren nach Quine und McCluskey vonnöten ist.
) verknüpft sind. Dabei müssen alle n Variablen der betrachteten n-stelligen booleschen Funktion im Konjunktionsterm vorkommen, um von einer Vollkonjunktion sprechen zu können. Vollkonjunktionen lassen sich zu einer disjunktiven Normalform zusammensetzen, was unter anderem beim Verfahren nach Quine und McCluskey vonnöten ist.Inhaltsverzeichnis
Beispiele
Beispiele für 3-stellige boolesche Funktionen
Standardnummerierung der Vollkonjunktionen
Vollkonjunktionen lassen sich auf natürliche Weise nummerieren. Man denkt sich dabei die Variablen in einer Reihe notiert, z. B. XnXn − 1...X2X1. Kommt für eine konkrete Vollkonjunktion das jeweilige Literal Xi negiert vor, so ersetzt man es durch eine 0, sonst durch eine 1. Es entsteht eine Binärzahl, die man dezimal interpretieren kann. Diese Dezimalzahl bezeichnet man als die Nummer oder den Index des Minterms. Will man diesen Minterm über seinen Index i bezeichnen, so schreibt man mi. Analog geht dies mit den Maxtermen Mi bei Disjunktionen.
Vergleich Minterm / Maxterm
In folgender Tabelle ist der Unterschied zwischen der Maxterm- und Mintermdarstellung ersichtlich:
Index x2 x1 x0 Minterm Maxterm 0 0 0 0 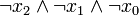
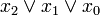
1 0 0 1 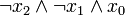
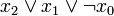
2 0 1 0 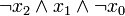
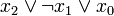
3 0 1 1 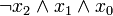
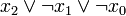
4 1 0 0 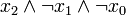
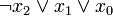
5 1 0 1 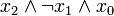
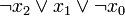
6 1 1 0 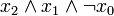
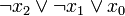
7 1 1 1 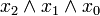
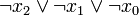
Realisierung von Decoder-Schaltungen mit Mintermen / Maxtermen:
Minterm Maxterm 0 NOR-Gatter AND-Gatter 1 OR-Gatter NAND-Gatter Bezug zum Karnaugh-Veitch-Diagramm
Man spricht auch vom Minterm einer Funktion F, wenn dieser F impliziert, d. h. wenn gilt
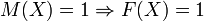 .
.
Dabei ist X der Vektor der Eingangsvariablen. Derartige Minterme M entsprechen umkehrbar eindeutig denjenigen Feldern eines Karnaugh-Veitch-Diagramms, die für die betrachtete Funktion den Wert 1 enthalten.
Siehe auch
Wikimedia Foundation.