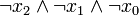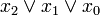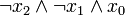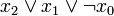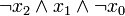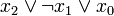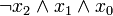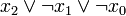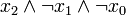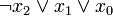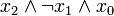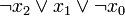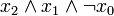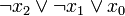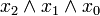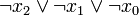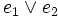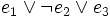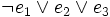Maxterm — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Maxterm — elementarioji disjunkcinė forma statusas T sritis automatika atitikmenys: angl. maxterm vok. Maxterm, m; Volldisjunktion, f rus. макстерм, m; элементарная дизъюнктивная форма, f pranc. terme disjoint, m … Automatikos terminų žodynas
maxterm — elementarioji disjunkcinė forma statusas T sritis automatika atitikmenys: angl. maxterm vok. Maxterm, m; Volldisjunktion, f rus. макстерм, m; элементарная дизъюнктивная форма, f pranc. terme disjoint, m … Automatikos terminų žodynas
Canonical form (Boolean algebra) — In Boolean algebra, any Boolean function can be expressed in a canonical form using the dual concepts of minterms and maxterms. Minterms are called products because they are the logical AND of a set of variables, and maxterms are called sums… … Wikipedia
K-Diagramm — Bild 1 1: Karnaugh Veitch Diagramm: ¬AB¬C¬D ∨ A¬B¬C¬D ∨ A¬B¬CD ∨ A¬BC¬D ∨ A¬BCD ∨ AB¬C¬D ∨ ABC¬D ∨ ABCD = AC ∨ B¬C¬D ∨ A¬B … Deutsch Wikipedia
KV-Algorithmus — Bild 1 1: Karnaugh Veitch Diagramm: ¬AB¬C¬D ∨ A¬B¬C¬D ∨ A¬B¬CD ∨ A¬BC¬D ∨ A¬BCD ∨ AB¬C¬D ∨ ABC¬D ∨ ABCD = AC ∨ B¬C¬D ∨ A¬B … Deutsch Wikipedia
KV-Diagramm — Bild 1 1: Karnaugh Veitch Diagramm: ¬AB¬C¬D ∨ A¬B¬C¬D ∨ A¬B¬CD ∨ A¬BC¬D ∨ A¬BCD ∨ AB¬C¬D ∨ ABC¬D ∨ ABCD = AC ∨ B¬C¬D ∨ A¬B … Deutsch Wikipedia
KV-Tafel — Bild 1 1: Karnaugh Veitch Diagramm: ¬AB¬C¬D ∨ A¬B¬C¬D ∨ A¬B¬CD ∨ A¬BC¬D ∨ A¬BCD ∨ AB¬C¬D ∨ ABC¬D ∨ ABCD = AC ∨ B¬C¬D ∨ A¬B … Deutsch Wikipedia
Karnaugh-Diagramm — Bild 1 1: Karnaugh Veitch Diagramm: ¬AB¬C¬D ∨ A¬B¬C¬D ∨ A¬B¬CD ∨ A¬BC¬D ∨ A¬BCD ∨ AB¬C¬D ∨ ABC¬D ∨ ABCD = AC ∨ B¬C¬D ∨ A¬B … Deutsch Wikipedia
Miniterm — Als Vollkonjunktion (auch: Minterm, Miniterm oder Elementarkonjunktion) bezeichnet man in der Aussagenlogik einen speziellen Konjunktionsterm, d. h. eine Anzahl von Buchstaben (Literalen), die alle durch ein logisches und ( ) verknüpft sind.… … Deutsch Wikipedia
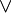 ) verknüpft sind. Dabei müssen alle n Variablen der betrachteten n-stelligen Booleschen Funktion im Disjunktionsterm vorkommen, um von einer Volldisjunktion sprechen zu können. Beispiele sind:
) verknüpft sind. Dabei müssen alle n Variablen der betrachteten n-stelligen Booleschen Funktion im Disjunktionsterm vorkommen, um von einer Volldisjunktion sprechen zu können. Beispiele sind: