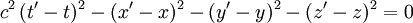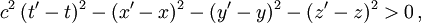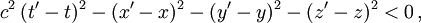Vorwärtskegel

In der relativistischen Physik bezeichnet der Lichtkegel eines Ereignisses E die Menge aller Ereignisse E', die sich mit Lichtgeschwindigkeit c auf E auswirken können oder von E mit Lichtgeschwindigkeit beeinflusst werden können.

Lichtkegel mit zwei raumartigen und einer zeitartigen Richtung

Seien (t,x,y,z) die Orts- und Zeitkoordinaten von 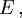$E\,,$ und (t',x',y',z') die Koordinaten von 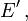$E'\,,$ dann liegt E' in der speziellen Relativitätstheorie auf dem Lichtkegel von 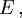$E\,,$ wenn der Differenzvektor mit Komponenten (t' − t,x' − x,y' − y,z' − z) lichtartig ist, das heißt, die Gleichung

$c^2\,(t' -t)^2 - (x' - x)^2 - (y' - y)^2 - (z' - z)^2 =0$

erfüllt.

Der Lichtkegel ist ein Doppelkegel im vierdimensionalen Minkowskiraum. Er besteht aus dem Vorwärtslichtkegel, das sind Ereignisse E', die später als E stattfinden, 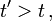$t' > t\,,$ und von E mit Lichtgeschwindigkeit verursacht worden sein können, und dem Rückwärtslichtkegel, der aus Ereignisse E' besteht, die vor E stattgefunden haben, 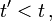$t' < t\,,$ und E mit Lichtgeschwindigkeit bewirkt haben können.

Ist der Differenzvektor zweier Ereignisse zeitartig, gilt also

$c^2\,(t' -t)^2 - (x' - x)^2 - (y' - y)^2 - (z' - z)^2 >0\,,$

so liegt das Ereignis E' im Inneren des Vorwärts- oder Rückwärtslichtkegels von E, je nachdem ob es nach oder vor E stattgefunden hat. Dann kann es sich bei E' um die Auswirkung oder die Ursache von E handeln, die sich langsamer als Licht auswirkt.

Ist der Differenzvektor zweier Ereignisse raumartig, gilt also

$c^2\,(t' -t)^2 - (x' - x)^2 - (y' - y)^2 - (z' - z)^2 <0\,,$

so kann es sich in der relativistischen Physik bei den Ereignissen nicht um Ursache und Wirkung handeln, denn dann müsste sich eine Ursache mit Überlichtgeschwindigkeit auswirken.

Die Lösung der inhomogenen Klein-Gordon-Gleichung hängt im Ereignis E nur von den früheren Anfangsbedingungen und der Imhomogenität auf dem Rückwärtslichtkegel von E und in seinem Inneren ab.

Verschwindet in der Klein-Gordon-Gleichung die Masse, handelt es sich spezieller um die Wellengleichung. Bei ihr wirken sich die Anfangsbedingungen und die Imhomogenität nur mit Lichtgeschwindigkeit aus, die Lösung hängt nur von den Anfangsbedingungen und der Imhomogenität auf dem Rückwärtslichtkegel von E ab.

Siehe auch

• Kausalität

Literatur

• Richard Courant und David Hilbert, Methoden der mathematischen Physik, Band 2, Springer Verlag, zweite Auflage 1968

Weblinks

• Norbert Dragon, Geometrie der Relativitätstheorie