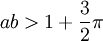- Weierstraßsche Funktion
-
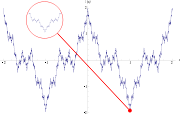 Graph einer reellen Weierstraß-Funktion im Intervall [ − 2,2]. Sie ist stetig, aber nirgends differenzierbar.
Graph einer reellen Weierstraß-Funktion im Intervall [ − 2,2]. Sie ist stetig, aber nirgends differenzierbar.In der Mathematik bezeichnet man als Weierstraß-Funktion ein pathologisches Beispiel einer reellwertigen Funktion der reellen Zahlengeraden. Die Funktion hat die Eigenschaft, dass sie überall stetig, aber nirgends differenzierbar ist. Sie ist nach ihrem Entdecker Karl Weierstraß benannt. Historisch gesehen liegt ihre Bedeutung darin, dass sie das erste publizierte Beispiel ist, das die übliche Meinung änderte, dass jede stetige Funktion differenzierbar bis auf eine Menge isolierter Punkte sei.
Intuitiv wurde seinerzeit angenommen, dass eine stetige Funktion eine Ableitung haben muss oder dass die Menge der Punkte, in denen sie nicht differenzierbar ist, „klein“ in irgendeinem Sinne ist. Frühere Mathematiker, einschließlich Carl Friedrich Gauß, haben oft angenommen, dass das wahr ist, wie Weierstraß in seiner Arbeit ausführt. Das rührt aus der Schwierigkeit, eine stetige Funktion zu zeichnen oder darzustellen, deren Menge nicht differenzierbarer Punkte etwas anderes ist als eine endliche Menge von Punkten. Es gibt jedoch Klassen von stetigen Funktionen, die sich besser verhalten, zum Beispiel die Lipschitz-stetigen Funktionen, deren Menge nicht-differenzierbarer Punkte eine Lebesgue-Nullmenge sein muss. Wenn man eine stetige Funktion zeichnet, dann entsteht üblicherweise der Graph einer Funktion, die Lipschitz-stetig ist und andere gutartige Eigenschaften besitzt, die nicht auf allgemeine, stetige Funktionen zutreffen.
Auch die weierstraßsche elliptische Funktion
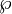 und die weierstraßsche sigma-, zeta- oder eta-Funktion werden manchmal als Weierstraß-Funktion bezeichnet.
und die weierstraßsche sigma-, zeta- oder eta-Funktion werden manchmal als Weierstraß-Funktion bezeichnet.Inhaltsverzeichnis
Definitionen von Weierstraß-Funktionen
Es gibt verschiedene ähnliche Definitionen einer Weierstraß-Funktion, die alle unendliche Reihen mit Winkelfunktionen sind. In Weierstraß' Originalarbeit wurde die Funktion durch
 mit 0 < a < 1 und
mit 0 < a < 1 und 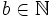
definiert, wobei zusätzlich
erfüllt sein muss.
Eine andere Definition ist
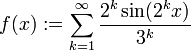 .
.
Anschaulich ist folgende Weierstraß-Funktion:
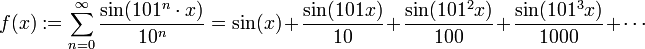 .
.
Ihr Graph sieht „fast“ so wie der der (differenzierbaren) Sinusfunktion aus. Und sie wäre auch differenzierbar, wenn nur noch endlich viele Summanden hinzukämen. Durch jeweils den nächsten (viel kleineren) Summanden wird der Graph um ein ganz kleines Stück verändert. Sie ist überall konvergent, stetig, aber man kann keine Tangenten zu ihr konstruieren, ist also nicht differenzierbar.
Die erste Definition, zusammen mit dem Beweis, dass sie nirgends differenzierbar ist, wurde von Weierstraß in einer Arbeit publiziert, die am 18. Juli 1872 bei der Königlichen Akademie der Wissenschaften eingereicht wurde.
Beweis der Stetigkeit
Für alle
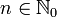 und
und 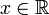 gilt
gilt 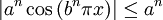 . Zudem ist die Reihe
. Zudem ist die Reihe 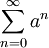 wegen 0 < a < 1 konvergent. Dann folgt aus dem weierstraßschen M-Test die (bezüglich
wegen 0 < a < 1 konvergent. Dann folgt aus dem weierstraßschen M-Test die (bezüglich 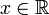 ) gleichmäßige Konvergenz von
) gleichmäßige Konvergenz von 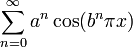 . Weil jeder einzelne Summand eine stetige Funktion ist und die Grenzfunktion einer gleichmäßig konvergenten Folge stetiger Funktionen wieder stetig sein muss, folgt daraus die behauptete Stetigkeit von f.
. Weil jeder einzelne Summand eine stetige Funktion ist und die Grenzfunktion einer gleichmäßig konvergenten Folge stetiger Funktionen wieder stetig sein muss, folgt daraus die behauptete Stetigkeit von f.Fraktale Eigenschaften
Die Weierstraß-Funktion kann vielleicht als eine der ersten Fraktale bezeichnet werden, obwohl dieser Begriff damals noch nicht verwendet wurde. Die Funktion ist auf jedem Niveau detailliert, so dass, wenn man in ein Stück der Kurve vergrößert, es sich nicht fortschreitend einer geraden Linie nähert. Unabhhängig davon wie dicht man zwischen zwei Punkte geht, die Funktion ist auf keinem noch so kleinen Intervall monoton. In seinem Buch Die Geometrie der fraktalen Mengen beobachtet Kenneth Falconer, dass die Hausdorff-Dimension der klassischen Weierstraß-Funktion nach oben durch
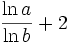 beschränkt ist, wobei a und b die Konstanten in der obigen Konstruktion sind, und es wird allgemein angenommen, dass es exakt dieser Wert ist, aber konnte bisher noch nicht bewiesen werden. Der Ausdruck Weierstraß-Funktion wird in der reellen Analysis oft verwendet, um sich auf irgendeine Funktion mit ähnlichen Eigenschaften und einer ähnlichen Konstruktion wie Weierstraß’ Originalbeispiel zu beziehen. Zum Beispiel kann die Kosinusfunktion in den unendlichen Reihen durch eine stückweise lineare „Zick-Zack-Funktion“ ersetzt werden. G.H. Hardy zeigte, dass die Funktion der obigen Konstruktion nirgends differenzierbar ist unter den Annahmen
beschränkt ist, wobei a und b die Konstanten in der obigen Konstruktion sind, und es wird allgemein angenommen, dass es exakt dieser Wert ist, aber konnte bisher noch nicht bewiesen werden. Der Ausdruck Weierstraß-Funktion wird in der reellen Analysis oft verwendet, um sich auf irgendeine Funktion mit ähnlichen Eigenschaften und einer ähnlichen Konstruktion wie Weierstraß’ Originalbeispiel zu beziehen. Zum Beispiel kann die Kosinusfunktion in den unendlichen Reihen durch eine stückweise lineare „Zick-Zack-Funktion“ ersetzt werden. G.H. Hardy zeigte, dass die Funktion der obigen Konstruktion nirgends differenzierbar ist unter den Annahmen 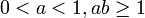 [1].
[1].Dichte nirgends differenzierbarer Funktionen
Es gibt unendlich viele stetige, nirgends differenzierbare Funktionen; die Weierstraß-Funktion ist nur das klassische Beispiel, bei der eine explizite Darstellung bekannt ist. Generell gilt:
- In der Topologie kann gezeigt werden, dass die Menge der nirgends differenzierbaren Funktionen auf dem Intervall [0,1] dicht liegt im Vektorraum
![C([0,1]; \R)](/pictures/dewiki/53/544765ec5d7a977bd4152d43e3c08c78.png) aller stetigen reellwertigen Funktionen auf dem Intervall [0,1] mit der Topologie der gleichmäßigen Konvergenz.
aller stetigen reellwertigen Funktionen auf dem Intervall [0,1] mit der Topologie der gleichmäßigen Konvergenz. - In der Maßtheorie zeigt sich zudem: Wenn der Raum
![C( [0,1]; \R)](/pictures/dewiki/53/544765ec5d7a977bd4152d43e3c08c78.png) mit der klassischen Wiener-Metrik γ ausgestattet ist, dann hat die Menge der Funktionen, die sogar in einem einzigen Punkt aus [0,1] differenzierbar ist, γ-Maß null. Dasselbe gilt, wenn man nur endlichdimensionale Teilmengen von
mit der klassischen Wiener-Metrik γ ausgestattet ist, dann hat die Menge der Funktionen, die sogar in einem einzigen Punkt aus [0,1] differenzierbar ist, γ-Maß null. Dasselbe gilt, wenn man nur endlichdimensionale Teilmengen von ![C([0,1]; \mathbb{R})](/pictures/dewiki/55/7c8500eaf07ec31b4035aaf383ef5923.png) nimmt: Die nirgends differenzierbaren Funktionen bilden eine prävalente Untermenge von
nimmt: Die nirgends differenzierbaren Funktionen bilden eine prävalente Untermenge von ![C([0,1]; \mathbb{R})](/pictures/dewiki/55/7c8500eaf07ec31b4035aaf383ef5923.png) .
.
Weblinks
Einzelnachweise
- ↑ Hardy G.H.: Weierstraß’ nicht differenzierbare Funktion. Trans. Amer. Math. Soc., Band 17, 1916, Seiten 301-325.
Wikimedia Foundation.