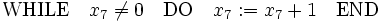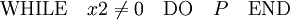While-Berechenbarkeit

WHILE-Programme spielen in der Theoretischen Informatik eine Rolle, insbesondere in Zusammenhang mit Berechenbarkeit.

Eigenschaften

• RAM-berechenbar, Turing-berechenbar, GOTO-berechenbar und WHILE-berechenbar sind äquivalent
• LOOP-berechenbar $\varsubsetneq$ WHILE-berechenbar
• Kleenesche Normalform (Jedes WHILE-Programm kommt auch nur mit einer While-Schleife aus)

Syntax

WHILE-Programme haben folgende Syntax in modifizierter Backus-Naur-Form:

$\begin{array}{lrl} P & ::= & x_i := x_j + c \\ & | & x_i := x_j - c \\ & | & P;P \\ & | & \mathrm{WHILE} \, x_i \ne 0 \, \mathrm{DO} \, P \, \mathrm{END} \end{array}$

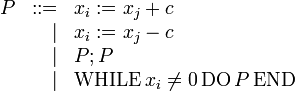
WHILE ist die Menge aller WHILE-Programme gemäß obiger Definition.

Jede WHILE-berechenbare Funktion ist GOTO-berechenbar und umgekehrt sowie turingberechenbar.

Erklärung der Syntax

Ein WHILE-Programm P besteht aus den Symbolen WHILE, DO, END, :=, +, -, ;, 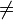$\ne$, einer Anzahl Variablen x₁,x₂,... sowie beliebigen Konstanten c.

Es sind nur drei verschiedene Anweisungen erlaubt, nämlich

• die Zuweisung einer Variablen durch eine weitere Variable, vermehrt um eine Konstante, etwa

x₃: = x₄ + 10

• oder vermindert um eine Konstante, etwa

x₅: = x₆ − 300

• eine WHILE-Anweisung, die eine Variable auf ungleich Null abfragt und ein WHILE-Programm zwischen DO und END enthält, etwa

$\mathrm{WHILE} \quad x_7 \ne 0 \quad \mathrm{DO} \quad x_7:=x_7+1 \quad\mathrm{END}$

Die Anweisungen sind für sich genommen bereits vollständige WHILE-Programme. Des weiteren ist die

• Aneinanderreihung von WHILE-Programmen, jeweils getrennt durch ein Semikolon

wieder ein WHILE-Programm.

Kleenesche Normalform für WHILE-Programme

Jede WHILE-berechenbare Funktion kann durch ein WHILE-Programm mit nur einer WHILE-Schleife berechnet werden.

Beweis: Sei P ein beliebiges WHILE-Programm. Wir formen P zunächst um, um ein äquivalentes GOTO-Programm P' zu erhalten und dann wieder zurück in ein äquivalentes WHILE-Programm P''. Per Konstruktion hat dieses nur eine WHILE-Schleife.

Konsequenzen

Die einfach beweisbare Tatsache, dass jedes GOTO-Programm in ein WHILE-Programm überführt werden kann und umgekehrt, hat zur Konsequenz, dass man beweisen kann, dass ein beliebiges Pascal-Programm die gleichen Leistungen erbringen kann wie ein beliebiges BASIC-Programm. Außerdem zeigt sie, dass man jedes Programm auch strukturiert programmieren kann, ohne „Spaghetticode“ zu erzeugen.

Simulation durch GOTO-Programm

Ein jedes WHILE-Programm

$\mathrm{WHILE} \quad x2 \ne 0 \quad\mathrm{DO} \quad P \quad\mathrm{END}$

kann durch das folgende GOTO-Programm simuliert werden:

M1: IF x2 = 0 THEN GOTO M2;
    P;
    GOTO M1;
M2: ...