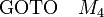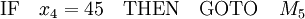Goto-Berechenbarkeit

GOTO-Programme sind spezielle Programme mit einer sehr einfachen Syntax. Dennoch spielen sie in Zusammenhang mit Berechenbarkeit eine große Rolle für die theoretische Informatik, insbesondere weil sich zeigen lässt, dass jede Turing-berechenbare Funktion GOTO-berechenbar ist.

Syntax

GOTO-Programme haben folgende Syntax in modifizierter Backus-Naur-Form:

• P:: = M₁:A;...;M_k:A
• $A ::= x_i := x_j + c \, | x_i := x_j - c \, | \, \mathrm{GOTO} \, M_i \, | \, \mathrm{IF} \, x_i = c \, \mathrm{THEN} \, \mathrm{GOTO} \, M_j \, | \, \mathrm{STOP}$
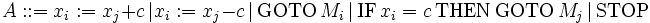
• M₁,...,M_k sind Marken (k ∈ ℕ)

GOTO ist die Menge aller GOTO-Programme gemäß obiger Definition.

Jede GOTO-berechenbare Funktion ist WHILE-berechenbar und umgekehrt.

Jede Turing-berechenbare Funktion ist GOTO-berechenbar.

Erklärung der Syntax

Jedes GOTO-Programm P besteht aus einer Anzahl von Anweisungen A, getrennt mit jeweils einem Semikolon. Vor jeder Anweisung befindet sich eine (eindeutige) Marke 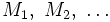$M_1,\ M_2,\ \dots$, gefolgt von einem Doppelpunkt.

GOTO-Programme haben eine endliche Anzahl von Variablen 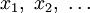$x_1,\ x_2,\ \dots$ und Konstanten c. Es sind nur fünf verschiedene Anweisungen erlaubt:

• Zuweisung einer Variablen durch eine weitere (dieselbe oder eine andere) Variable, vermehrt um eine Konstante, etwa

x₁: = x₂ + 3

• oder vermindert um eine Konstante, etwa

x₃: = x₃ − 1.

• eine Sprunganweisung

$\mathrm{GOTO} \quad M_4$

• eine bedingte Sprunganweisung, wobei eine Variable auf Gleichheit mit einer Konstanten abgefragt wird, etwa

${\rm IF} \quad x_4 = 45 \quad {\rm THEN} \quad {\rm GOTO} \quad M_5$

• und die STOP-Anweisung

STOP.

Konsequenz

Damit kann man formal zeigen, dass jedes BASIC-Programm auch durch ein äquivalentes Pascal-, C-, C++- oder Java-Programm dargestellt werden kann.

Simulation durch WHILE-Programm

Ein jedes GOTO-Programm

M1: A1; M2: A2; ... Mk: Ak

kann durch ein WHILE-Programm der folgenden Form simuliert werden

counter := 1;
WHILE counter != 0 DO
  IF counter = 1 THEN B1 END;
  IF counter = 2 THEN B2 END;
  ...
  IF counter = k THEN Bk END;
END

wobei

Bi = xj := xn + c; counter := counter + 1   falls Ai = xj := xn + c
Bi = xj := xn - c; counter := counter + 1   falls Ai = xj := xn - c
Bi = counter := n                           falls Ai = GOTO Mn
Bi = IF xj = c THEN counter = n
     ELSE counter = counter + 1             falls Ai = IF xj = c THEN GOTO Mn
     END
Bi = counter := 0                           falls Ai = STOP

Siehe auch

• Sprunganweisung (GOTO)
• LOOP-Programm
• WHILE-Programm
• µ-Rekursion