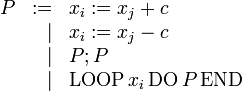Loop-Berechenbarkeit

LOOP-Programme sind Programme in der Programmiersprache LOOP, einer stark eingeschränkten, modellhaften Sprache, die nur die Formulierung von Additionen, Wertzuweisungen und endlich oft durchlaufenen Schleifen erlaubt. LOOP-Programme spielen in der Theoretischen Informatik eine Rolle, insbesondere in Zusammenhang mit Berechenbarkeit. Eine Funktion heißt LOOP-berechenbar, wenn sie sich als LOOP-Programm formulieren lässt. Die Menge aller LOOP-Programme wird mit LOOP bezeichnet.

Eigenschaften

Jede primitiv-rekursive Funktion ist LOOP-berechenbar und umgekehrt^[1].

Im Unterschied zu GOTO-Programmen und WHILE-Programmen terminieren LOOP-Programme immer^[2]. Deswegen ist die Menge der durch LOOP-Programme berechenbaren Funktionen eine echte Untermenge der berechenbaren Funktionen (und damit eine Untermenge der durch WHILE- bzw. GOTO-Programme berechenbaren Funktionen)^[3].

Ein Beispiel für eine berechenbare aber nicht LOOP-berechenbare totale Funktion ist die Ackermann-Funktion^[4].

Formale Definition

Syntax

LOOP-Programme bestehen aus den Symbolen LOOP, DO, END, :=, +, - und ; sowie einer beliebigen Anzahl von Variablen und Konstanten. LOOP-Programme haben folgende Syntax in modifizierter Backus-Naur-Form:

$\begin{array}{lrl} P & := & x_i := x_j + c \\ & | & x_i := x_j - c \\ & | & P;P \\ & | & \mathrm{LOOP} \, x_i \, \mathrm{DO} \, P \, \mathrm{END} \end{array}$

Hierbei sind Var: = {x₀,x₁,...} Variablennamen und 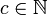$c \in \mathbb{N}$ Konstanten.

Semantik

Ein Ausdruck der Form

x0 := x1 + c

bedeutet die Zuweisung des um c erhöhten Wertes der Variablen x₁ an die Variable x₀. Dabei ist für c der Wert Null zulässig, so dass sich auch die direkte Zuweisung des Wertes einer Variablen an eine andere Variable mit diesem syntaktischen Konstrukt formulieren lässt:

x0 := x1 + 0

Ein Ausdruck der Form

x0 := x1 - c

bedeutet die Zuweisung des um c verminderten Wertes der Variablen x₁ an die Variable x₀. Bei der Ausführung von Zuweisungen werden negative Werte implizit durch Nullen ersetzt.

Variablen dürfen in Zuweisungsausdrücken gleichzeitig auf der linken und auf der rechten Seite des Symbols := erscheinen. Ein Ausdruck der Form

x := x + c

erhöht beispielsweise den Wert der Variablen x um c.

Die in einem LOOP-Programm verwendeten Variablen werden vor Beginn des Programmablaufs mit vorgegeben Initialwerten vorbelegt.

Ein Ausdruck der Form

P1; P2

bedeutet die Hintereinanderausführung der Teilprogramme P₁ und P₂ in dieser Reihenfolge. Ein Ausdruck der Form

LOOP x DO P END

bedeutet die x-fache Ausführung des Teilprogramms P, wobei x den Wert am Beginn der Abarbeitung darstellt. (Auch wenn x durch die Ausführung von P verändert wird, wird P nur so oft ausgeführt, wie x am Anfang war.) Hat x dabei den Wert Null, so wird das Teilprogramm P innerhalb des LOOP-Ausdrucks überhaupt nicht ausgeführt. Dieser Umstand erlaubt die Formulierung von Verzweigungen in LOOP-Programmen durch die bedingte Ausführung von Teilprogrammen in Abhängigkeit vom Wert einer Variablen.

Beispielprogramme

Addition

Das folgende LOOP-Programm weist der Variablen x₀ die Summe der Werte der Variablen x₁ und x₂ zu.

x0 := x1 + 0;
LOOP x2 DO
   x0 := x0 + 1
END

Dabei bekommt zunächst x₀ den aktuellen Wert von x₁ zugewiesen und wird dann um den Wert von x₂ inkrementiert.

Dieses Programm lässt sich als Unterprogramm in anderen LOOP-Programmen verwenden. Solche Verwendungen werden durch eine einfache Erweiterung der ursprünglichen LOOP-Syntax in der Form

x0 := x1 + x2

beschrieben.

Multiplikation

Das folgende LOOP-Programm erhöht den Wert der Variablen x₀ um den Wert des Produktes der Werte der Variablen x₁ und x₂.

LOOP x1 DO
  x0 := x0 + x2
END

Das Programm benutzt dabei das im ersten Beispiel definierte Unterprogramm der Addition. Die ausgeführte Multiplikation wird dabei durch das x₁-fache Aufaddieren des Wertes von x₂ zum Wert von x₀ realisiert.

Simulation von LOOP-Programmen durch WHILE-Programm

Ein jedes LOOP-Programm

LOOP x DO P END

kann durch das folgende WHILE-Programm simuliert werden

y := x
WHILE y != 0 DO y := y-1; P END

Siehe auch

• µ-Rekursion

Einzelnachweise

1. ↑ Schöning, 2001, S. 113
2. ↑ Schöning, 2001, S. 101
3. ↑ Schöning, 2001, S. 122
4. ↑ Schöning, 2001, S. 102, S. 120

Literatur

• Uwe Schöning: Theoretische Informatik - kurzgefasst. 4. Auflage. Spektrum Akademischer Verlag, 2001, ISBN 3-8274-1099-1.