- Winkelsymmetrale
-
In der Geometrie ist die Winkelhalbierende (auch Winkelsymmetrale genannt) eines Winkels die Halbgerade, die durch den Scheitelpunkt des Winkels läuft und den Winkel in zwei gleiche Teile teilt.
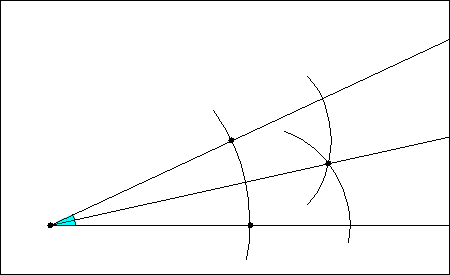
Konstruktion: Sie kann mit einem Zirkel und einem Lineal (Geodreieck) konstruiert werden. Dabei wird um den Scheitelpunkt ein Kreis mit beliebigem Radius gezeichnet. An den Schnittpunkten mit den Schenkeln des Winkels wird der Zirkel erneut angesetzt. Dann zeichnet man jeweils einen Kreis mit gleichem Radius. Die Schnittpunkte dieser zwei Kreise liegen auf der Winkelhalbierenden.
Liegen allgemeiner zwei Geraden vor, die sich in einem Punkt schneiden, so haben wir vier Winkel und damit vier Winkelhalbierende. Die Winkelhalbierenden zweier Scheitelwinkel fallen zusammen; also bleiben nur zwei Winkelhalbierenden übrig. Diese zwei Winkelhalbierenden - die zueinander orthogonal sind - nennt man die Winkelhalbierenden der zwei Geraden.
Die Winkelhalbierenden von zwei Geraden sind Symmetrieachsen der Figur, die aus den zwei Geraden besteht. Das heißt, zwei Geraden sind immer zueinander symmetrisch bezüglich jeder von ihren beiden Winkelhalbierenden. Deshalb heißen die letzteren auch Winkelsymmetralen.
Die Vereinigung der beiden Winkelhalbierenden von zwei Geraden ist die Menge aller Punkte, die von den beiden Geraden den gleichen Abstand haben, oder, anders formuliert, die Menge der Mittelpunkte aller Kreise, die die beiden Geraden berühren.
Wenn wir wieder zu dem Fall eines Winkels zurückkommen, der von zwei Schenkeln (Halbgeraden) begrenzt wird, und nun diese Schenkel zu Geraden verlängern, dann bekommen wir zwei Geraden mit zwei Winkelhalbierenden. Die eine davon ist die Winkelhalbierende des ursprünglichen Winkels; die andere ist die Winkelhalbierende seines Nebenwinkels; sie heißt Außenwinkelhalbierende des ursprünglichen Winkels.
Inhaltsverzeichnis
Winkelhalbierende im Dreieck
Ist in der Dreieckslehre von Winkelhalbierenden die Rede, so bezieht sich dieser Begriff meist auf die Innenwinkel, seltener auf die Außenwinkel. Für diese Winkelhalbierenden gelten unter anderem folgende Sätze:
- Die drei Winkelhalbierenden (der Innenwinkel) eines Dreiecks schneiden sich in einem Punkt. Dieser Punkt ist der Mittelpunkt des Inkreises (siehe auch: Ausgezeichnete Punkte im Dreieck).
- Jede Winkelhalbierende (eines Innenwinkels) im Dreieck teilt die gegenüberliegende Seite im Verhältnis der anliegenden Seiten. (Diese Aussage lässt sich mithilfe ähnlicher Dreiecke oder durch Anwendung des Sinussatzes beweisen.)
- Die Halbierenden eines Innenwinkels und der zu den beiden anderen Innenwinkeln gehörenden Außenwinkel eines Dreiecks schneiden sich jeweils in einem Punkt. Dieser Punkt ist der Mittelpunkt eines Ankreises.
- Die Schnittpunkte der Außenwinkelhalbierenden mit den verlängerten Gegenseiten der entsprechenden Innenwinkel liegen, sofern sie existieren, auf einer Geraden.
Winkelhalbierende im Viereck
Die Winkelhalbierenden eines Vierecks begrenzen im Allgemeinen ein Sehnenviereck. Beim Sehnenviereck ist dieses Viereck zugleich Tangentenviereck. Beim Tangentenviereck ist es zu einem Punkt entartet. Die Winkelhalbierenden eines Parallelogramms schließen im Allgemeinen ein Rechteck ein, die Winkelhalbierenden eines Rechtecks im Allgemeinen ein Quadrat.
Winkelhalbierende im Koordinatensystem
In einem kartesischen Koordinatensystem spielen die beiden Winkelhalbierenden der Koordinatenachsen eine besondere Rolle:
Als 1. Winkelhalbierende (Winkelhalbierende des I. und III. Quadranten) bezeichnet man den Graphen der Funktion f(x)=x. Dieser Graph ist die Ursprungsgerade mit der Steigung 1.
Als 2. Winkelhalbierende (Winkelhalbierende des II. und IV. Quadranten) bezeichnet man den Graphen der Funktion f(x)=-x. Dieser Graph ist die Ursprungsgerade mit der Steigung -1.
Weblinks
- Klassische Transversalen - Innen- und Außenwinkelhalbierende unter D.7
Wikimedia Foundation.