Euler'sche Gerade

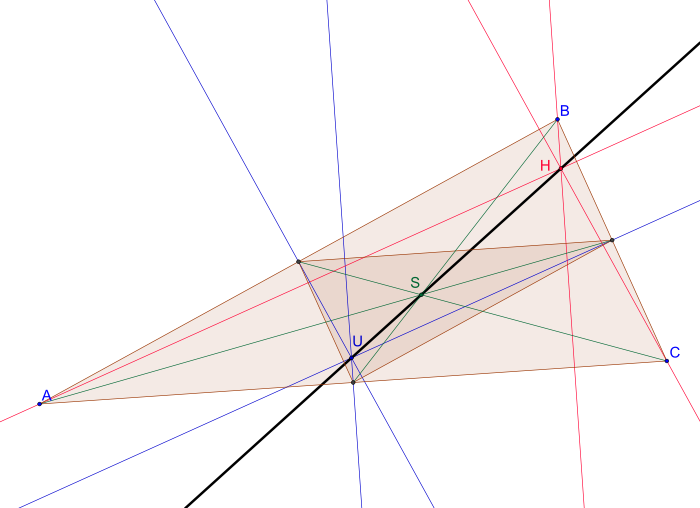
Unter der eulerschen Geraden eines Dreiecks (auch Eulergeraden, benannt nach dem Mathematiker Leonhard Euler) versteht man die Gerade, die durch den Schwerpunkt, den Umkreismittelpunkt und den Höhenschnittpunkt des Dreiecks geht.

Außerdem gilt 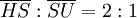$\overline{HS}: \overline{SU} = 2: 1$, wobei der Punkt S zwischen den Punkten H und U liegt. Die eulersche Gerade geht auch durch den Mittelpunkt des Feuerbachkreises; der Mittelpunkt dieses Kreises ist gleichzeitig der Mittelpunkt der Strecke [HU].

In einem gleichschenkligen Dreieck stimmt die eulersche Gerade mit der zur Basis gehörigen Seitenhalbierenden (Mittelsenkrechten, Höhe, Winkelhalbierenden) überein. Im Falle eines gleichseitigen Dreiecks kann man nicht mehr von der eulerschen Geraden sprechen, weil dann die drei bestimmenden Punkte S, U und H zu einem Punkt zusammenfallen. (Sie liegen dann auf unendlich vielen Geraden, d. h. jede Gerade durch diesen einen Punkt könnte als eulersche Gerade aufgefasst werden, was man aber der Eindeutigkeit halber vermeidet.)

Auf der eulerschen Geraden des Dreiecks ABC liegt auch der Umkreismittelpunkt des Dreiecks, das von den Tangenten an den Umkreis des Dreiecks ABC in den Punkten A, B und C gebildet wird. Darüber hinaus enthält die eulersche Gerade noch weitere ausgezeichnete Punkte des Dreiecks, unter anderem den Longchamps-Punkt und den Schiffler-Punkt.

Weblinks

• Eric W. Weisstein: Euler Line auf MathWorld (englisch)
• Eulersche Gerade - zwei dynamische Konstruktionen der eulerschen Geraden mit Hilfe von GeoGebra.
• Dynamische Konstruktion - eine Visualisierung der eulerschen Geraden mit Hilfe von GeoGebra.

Literatur

• Max Koecher, Aloys Krieg: Ebene Geometrie, 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3