Südpolsatz

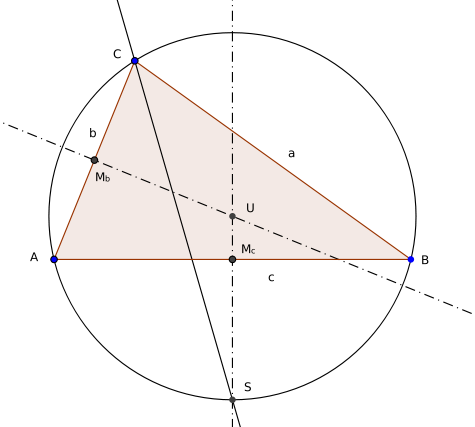
Der Südpolsatz ist ein geometrischer Satz aus der Dreieckslehre. Er besagt, dass sich in einem Dreieck die Mittelsenkrechte (Streckensymmetrale) einer Seite und die Winkelhalbierende (Winkelsymmetrale) durch die gegenüberliegende Ecke immer auf dem Umkreis schneiden. Der Schnittpunkt wird auch Südpol genannt.

Beweis

Der Satz soll für die Mittelsenkrechte m_c und die Winkelhalbierende w_γ begründet werden. S sei definiert als derjenige Schnittpunkt der Mittelsenkrechten m_c mit dem Umkreis, der nicht auf der gleichen Seite von AB liegt wie die Ecke C. Ist U der Umkreismittelpunkt, so ist der Winkel ACS ist halb so groß wie der Winkel AUS, da es sich um den Umfangswinkel (Peripheriewinkel) und Mittelpunktswinkel (Zentriwinkel) über dem Kreisbogen AS handelt. Entsprechend ist der Winkel SCB halb so groß wie der Winkel SUB. Da die Winkel AUS und SUB aus Symmetriegründen gleich groß sind, müssen auch die Winkel ACS und SCB gleich groß sein. Mit anderen Worten: S muss auf der Winkelhalbierenden des Winkels $\gamma = \angle ACB$ liegen. Der Schnittpunkt der Mittelsenkrechten und der Winkelhalbierenden muss also mit S übereinstimmen und folglich auf dem Umkreis liegen.

Weblinks

• Südpolsatz - eine Visualisierung mit dem dynamischen Geometrieprogramm GeoGebra