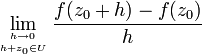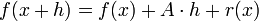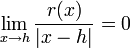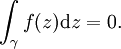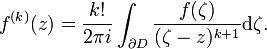Wirtinger-Ableitung

Holomorphie (von gr. holos, „ganz“ und morphe , „Form“) ist eine Eigenschaft von bestimmten komplexwertigen Funktionen, die in der Funktionentheorie (einem Teilgebiet der Mathematik) behandelt werden. Eine Funktion 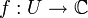$f: U \rightarrow \mathbb{C}$ für eine offene Menge 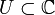$U \subset \mathbb{C}$ heißt holomorph, falls sie in jedem Punkt aus U komplex differenzierbar ist.

Auch wenn die Definition analog zur reellen Differenzierbarkeit ist, zeigt sich in der Funktionentheorie, dass die Holomorphie eine sehr starke Eigenschaft ist. Sie produziert nämlich eine Vielzahl von Phänomenen, die im Reellen kein Pendant besitzen. Beispielsweise ist eine holomorphe Funktion stets unendlich oft differenzierbar und lässt sich lokal in jedem Punkt in eine Potenzreihe entwickeln.

Definitionen

Es sei 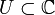$U \subset \mathbb{C}$ eine offene Teilmenge der komplexen Ebene und 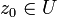$z_0\in U$ ein Punkt dieser Teilmenge. Eine Funktion 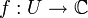$f:U \rightarrow \mathbb{C}$ heißt komplex differenzierbar im Punkt z₀, falls der Grenzwert

$\lim_{{h \rightarrow 0}\atop{h+z_0 \in U}}\frac{f(z_0+h)-f(z_0)}{h}$

existiert. In diesem Fall bezeichnet man diesen Grenzwert als $\ f'(z_0)$.

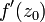Die Funktion f heißt holomorph im Punkt z₀, falls eine Umgebung von z₀ existiert, in der f komplex differenzierbar ist. Ist f auf ganz $\mathbb{C}$ holomorph, so nennt man f eine ganze Funktion.

Erläuterungen

Unterschied zwischen komplexer und reeller Differenzierbarkeit

Zu beachten ist, dass es, im Gegensatz zu reeller Differenzierbarkeit, nicht nur zwei, sondern unendlich viele Möglichkeiten gibt, sich dem Punkt z zu nähern. Komplexe Differenzierbarkeit ist also eine starke Eigenschaft.

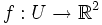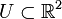Nicht jede reell differenzierbare Funktion $f: U \rightarrow \mathbb{R}^2$ mit $U \subset \mathbb{R}^2$ ist also, wenn man sie in naheliegender Weise als Funktion auf $\mathbb{C}$ auffasst, auch holomorph. Im Reellen heißt eine Funktion differenzierbar, falls eine $\mathbb{R}$-lineare Abbildung A existiert, so dass die Gleichung

$f(x+h) = f(x) + A\cdot h + r(x)$

gilt, wobei r eine Funktion mit

$\lim_{x \rightarrow h} \frac{r(x)}{|x-h|} = 0$

ist. Für holomorphe Funktionen muss A natürlich $\mathbb{C}$-linear sein, was eine starke Einschränkung bedeutet.

Zusammenhang zwischen komplexer und reeller Differenzierbarkeit

Eine Funktion 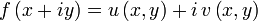$f\left(x+iy\right)=u\left(x,y\right) + i\,v\left(x,y\right)$ ist genau dann komplex differenzierbar, wenn u,v stetig partiell differenzierbar sind und die cauchy-riemannschen Differentialgleichungen

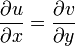$\frac{\partial u}{\partial x}= \frac{\partial v}{\partial y}$ und $\frac{\partial u}{\partial y}= -\frac{\partial v}{\partial x}$

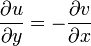
erfüllt sind.

Beispiele

Folgende Funktionen sind holomorph auf ganz $\mathbb{C}$:

• jedes Polynom 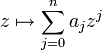$z\mapsto\sum\limits_{j=0}^na_jz^j$ mit Koeffizienten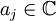 $a_j \in \mathbb{C}$

• die Exponentialfunktion exp

• die trigonometrischen Funktionen sin und cos

• die hyperbolischen Funktionen sinh und cosh

Folgende Funktionen sind in keinem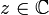 $z\in\mathbb{C}$ komplex differenzierbar und damit auch nirgendwo holomorph:

• die Betragsfunktion $z\mapsto |z|$

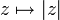
• die Projektionen auf den Realteil 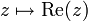$z\mapsto\mathrm{Re}(z)$ beziehungsweise auf den Imaginärteil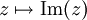 $z\mapsto\mathrm{Im}(z)$

• die komplexe Konjugation $z\mapsto\overline{z}$

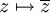
Eigenschaften

Hier folgt eine Auflistung fundamentaler Eigenschaften holomorpher Funktionen, die allesamt kein Pendant in der reellen Theorie besitzen. In der Folge sei 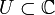$U \subset \mathbb C$ ein Gebiet und 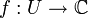$f: U \rightarrow \mathbb C$ holomorph.

Cauchyscher Integralsatz

Ist 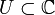$U \subset \mathbb{C}$ einfach zusammenhängend und γ ein Zyklus in U, so gilt der cauchysche Integralsatz

$\int_\gamma f(z)\mathrm dz=0\!\,.$

Cauchysche Integralformel

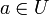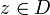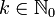• Sei D: = U_r(a) die offene Kreisscheibe mit Radius r um den Punkt $a \in U$, die ganz in U liegt. Dann gilt für alle $z \in D$ und $k \in\N_0$ die cauchysche Integralformel

$f^{(k)}(z) = \frac{k!}{2\pi i}\int_{\partial D}\frac{f(\zeta)}{(\zeta-z)^{k+1}}\mathrm d\zeta.$

Der Funktionswert eines Punktes in einem Gebiet hängt also nur von den Funktionswerten am Rand dieses Gebietes ab. Für mehrdimensionale holomorphe Abbildungen gibt es ein Analogon. Dieses ist unter dem Namen bochner-martinellische Integralformel bekannt.

Holomorphie und Analytizität

Eine Folgerung aus der cauchyschen Integralformel ist, dass in der komplexen Ebene der Begriff der Analytizität äquivalent zur Holomorphie ist: Jede in z₀ holomorphe Funktion ist in z₀ analytisch. Umgekehrt lässt sich jede in z₀ analytische Funktion zu einer in z₀ holomorphen Funktion fortsetzen.

Da Potenzreihen unendlich oft komplex differenzierbar sind (und zwar durch gliedweise Differentiation), erhält man insbesondere, dass holomorphe Funktionen unendlich oft differenzierbar und alle ihre Ableitungen wiederum holomorphe Funktionen sind. Hieran erkennt man schon deutliche Unterschiede zur reellen Differentialrechnung.

Identitätssatz

Es zeigt sich, dass eine holomorphe Funktion schon durch sehr wenig Information eindeutig bestimmt ist. Der Identitätssatz besagt, dass zwei holomorphe Funktionen auf einem Gebiet 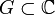$G \subset \C$ bereits dann auf G identisch sind, wenn sie auf einer geeigneten Teilmenge 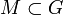$M \subset G$ übereinstimmen. Dabei muss die Übereinstimmungsmenge M noch nicht mal ein kontinuierlicher Weg sein, es reicht aus, dass M einen Häufungspunkt in G besitzt. Diskrete Teilmengen reichen hierfür hingegen nicht aus.

Weiteres

• Der Satz von Liouville besagt, dass jede beschränkte ganze Funktion konstant ist. Eine einfache Folgerung hieraus ist der Fundamentalsatz der Algebra.

• Ist 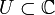$U \subset \mathbb C$ ein Gebiet und 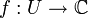$f:U \rightarrow \mathbb C$ nicht konstant, dann ist 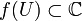$f(U)\subset\mathbb C$ wieder ein Gebiet. (Satz von der Gebietstreue)

• Eine Folgerung der Gebietstreue ist das Maximumprinzip.

• Konvergiert eine Folge 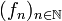$(f_n)_{n \in \mathbb{N}}$ holomorpher Funktionen kompakt auf U gegen die Grenzfunktion f, so ist f wieder holomorph, und man kann Limesbildung und Differentiation vertauschen, das heißt, die Folge (f'_n) konvergiert kompakt gegen f'. (Satz von Weierstraß).

• Ist die Folge 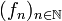$(f_n)_{n \in \mathbb{N}}$ holomorpher Funktionen auf U lokal beschränkt, so existiert eine kompakt konvergente Teilfolge. (Satz von Montel)

Biholomorphe Funktionen

Eine Folgerung des Satzes über implizite Funktionen ist, dass für eine holomorphe Funktion, die bijektiv ist, stets auch die Umkehrabbildung holomorph ist. Eine holomorphe und bijektive Abbildung heißt biholomorph.

Holomorphie mehrerer Veränderlicher

Sei 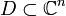$D \subset \mathbb{C}^n$ eine komplexe offene Teilmenge. Eine Abbildung 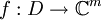$f:D \rightarrow \mathbb{C}^m$ heißt holomorph, falls 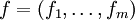$f = (f_1, \ldots , f_m)$ in jeder Teilfunktion und jeder Variablen holomorph ist.

Seien

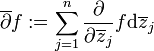$\overline{\partial} f := \sum_{j=1}^n \frac{\partial}{\partial \overline{z}_j} f {\rm d} \overline{z}_j\$ und

$\partial f := \sum_{j=1}^n \frac{\partial}{\partial z_j} f {\rm d} z_j$

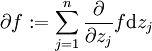
die Dolbeault-Operatoren. Eine äquivalente Definition der Holomorphie einer Funktion f lautet 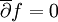$\overline{\partial} f = 0$, und für die Ableitungsfunktion gilt

$\frac{{\rm d}}{{\rm d}z} f = \overline{\partial} f + \partial f$.

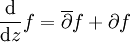Hierbei bezeichnen 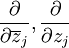$\frac{\partial}{\partial \overline{z}_j}, \frac{\partial}{\partial z_j}$ die Wirtingerableitungen, welche definiert sind als

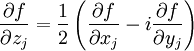$\frac{\partial f}{\partial z_j} = \frac{1}{2} \left(\frac{\partial f}{\partial x_j} - i\frac{\partial f}{\partial y_j}\right)$ und

$\frac{\partial f}{\partial \overline{z}_j} = \frac{1}{2} \left(\frac{\partial f}{\partial x_j} + i\frac{\partial f}{\partial y_j}\right)$.

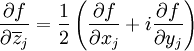Die Äquivalenz der Definitionen ist leicht mit Hilfe der cauchy-riemannschen Differentialgleichungen zu erkennen.

Literatur

Standardwerke

Einführungen

• Klaus Jänich: (Die ersten beiden Auflagen unterscheiden sich deutlich von den folgenden. Unter anderem fehlen ab der dritten Auflage die vier „Stern“-Kapitel zu Wirtinger-Kalkül, riemannschen Flächen, riemannschen Flächen eines holomorphen Keimes und algebraischen Funktionen.)

• Einführung in die Funktionentheorie. 2. Auflage. Springer-Verlag, Berlin/Heidelberg 1980, ISBN 3-540-10032-6. 

• Funktionentheorie – Eine Einführung. 6. Auflage. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 3-540-20392-3. 

• Wolfgang Fischer, Ingo Lieb: Funktionentheorie – Komplexe Analysis in einer Veränderlichen. 8. Auflage. Vieweg, Braunschweig/Wiesbaden 2003, ISBN 3-528-77247-6. 

Ausführliche Darstellungen der Funktionentheorie

• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3. Auflage. Springer, 2000, ISBN 3-540-67641-4. 

• Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, Heidelberg 2002, ISBN 3-540-41855-5. 

Siehe auch

Komplexe Teilmengen, Konforme Abbildung