- Bekundete Präferenz
-
Die Theorie der Revealed Preference (auf deutsch etwa: Offenbarte Präferenz oder Bekundete Präferenz) wurde maßgeblich von Paul A. Samuelson entwickelt, um Konsumentenentscheidungen daraufhin zu untersuchen, ob sie einem konsequenten Muster folgen, bzw. (technischer ausgedrückt), ob die Entscheidungen durch eine Nutzenfunktion mit bestimmten Eigenschaften entstanden sein können. Die Theorie der Revealed Preference ist eng verbunden mit der Haushaltstheorie bzw. der Konsumententheorie in der Mikroökonomie. Sie wurde unter anderem von Hendrick Houthakker und Hal R. Varian weiterentwickelt.
Das Konzept der Nutzenfunktion ist abstrakt: Welcher Konsument ist sich schon bewusst, mit einer ordentlich definierten Funktion zu existieren, die alle Konsumentscheidungen bestimmt? Man kann auch mit einiger Berechtigung fragen, ob Konsumenten wirklich vollständig konsequent und rational entscheiden. Es gibt viele Gründe, warum das nicht so zu sein braucht. Dazu ein Beispiel (aus Mas-Colell et al. 1995): Fragen wir jemanden, mit welcher Farbe er seine Wohnung streichen möchte, und geben ihm zwei sehr ähnliche Grautöne zur Auswahl, so kann es sein, dass er die beiden Töne nicht auseinanderhalten kann und sagt, er sei indifferent. Nehmen wir dann den helleren Grauton und legen einen noch helleren Grauton daneben, wird er ebenfalls indifferent sein, wenn er wieder keinen Unterschied feststellen kann. Wenn man so weitermacht und am Ende den hellsten Grauton neben dem zu Anfang benutzten dunklen Grauton hält, so kann es sein, dass sich nun eine eindeutige Präferenz zugunsten einer der beiden Töne ergibt. Damit hätte man eine Reihe von Präferenzen erzeugt, die die Transitivitätsannahme verletzt.
Gewöhnlich lässt sich die Nutzenfunktion eines Konsumenten nicht direkt beobachten (sofern sie überhaupt vorhanden ist). Man kann bestenfalls eine Reihe von (Konsum-)Entscheidungen (bei verschiedenen Preisen) beobachten. Angenommen, im obigen Beispiel wäre die letzte Entscheidung zugunsten des helleren Grautons ausgefallen. Damit lässt sich dann sagen, dass der Konsument den helleren Grauton gegenüber dem dunkleren im direkten Vergleich bevorzugt. Der hellere Ton ist also directly revealed preferred.
Angenommen, der Konsument soll sich nun zwischen Rot und Blau entscheiden, und er wählt Rot. Danach soll er sich zwischen Rot und Grün entscheiden, und er wählt Grün. Nun haben wir zwei directly revealed preferred-Relationen, können aber noch mehr sagen: Aufgrund der Transitivitätsannahme darf es keine kreisförmigen Relationen geben. Das heißt, wenn Rot gegenüber Blau bevorzugt wird, und Grün gegenüber Rot, dann können wir auch sagen, dass Grün gegenüber Blau bevorzugt wird. Grün ist in diesem Fall (indirectly) revealed preferred.
Formale Darstellung
Anmerkung: Die Art der Darstellung variiert von Lehrbuch zu Lehrbuch, von Artikel zu Artikel. Im folgenden wird grob der Schreibweise von Varian (1992) gefolgt, die wiederum Ähnlichkeiten mit Houthakker (1950) aufweist.
Es seien
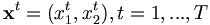 die gewählten Mengen zweier Güter zum Zeitpunkt t. Es seien
die gewählten Mengen zweier Güter zum Zeitpunkt t. Es seien 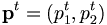 die zugehörigen Preise. Nun können zwei Konzepte definiert werden:
die zugehörigen Preise. Nun können zwei Konzepte definiert werden:Directly Revealed Preference:
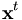 ist directly preferred gegenüber
ist directly preferred gegenüber 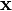 wenn
wenn 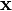 gewählt werden konnte, aber
gewählt werden konnte, aber 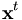 tatsächlich gewählt wurde. Dafür schreiben wir
tatsächlich gewählt wurde. Dafür schreiben wir 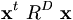 . Formale Definition:
. Formale Definition: 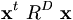 dann und nur dann, wenn
dann und nur dann, wenn 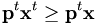 .
.Revealed Preference: Ist eine Reihe von directly preferred-Relationen gegeben, so dass
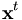 directly revealed preferred gegenüber
directly revealed preferred gegenüber 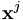 , was wiederum directly revealed preferred gegenüber
, was wiederum directly revealed preferred gegenüber 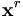 , ... gegenüber
, ... gegenüber 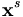 was wiederum directly preferred gegenüber
was wiederum directly preferred gegenüber 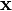 ist bei t,j,r,...,s sagen wir, dass
ist bei t,j,r,...,s sagen wir, dass 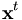 (indirectly) revealed preferred gegenüber
(indirectly) revealed preferred gegenüber 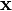 ist und schreiben
ist und schreiben 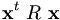 . Formale Definition:
. Formale Definition: 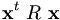 dann und nur dann, wenn
dann und nur dann, wenn 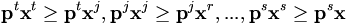 .
.
Ergänze: Axiome.Literatur
Houthakker, Hendrick S. (1950): Revealed Preference and the Utility Function, Economica, 17, 159-174
Schönfeld, Peter (1962): Grundzüge der Theorie der faktischen Präferenz, Journal of Economics, Volume 22, Number 3 / September 1962
Mas-Colell, Andreu, Whinston, Michael D., Green, Jerry R. (1995): Microeconomic Theory. New York: Oxford
Samuelson, Paul A. (1938): A Note on the Pure Theory of Consumer's Behaviour, Economica, 5, 61-71
Samuelson, Paul A. (1948): Consumption Theory in Terms of Revealed Preference, Economica, 15, 243-253
Varian, Hal R. (1982): The Nonparametric Approach to Demand Analysis, Econometrica, 50, 945-972
Varian, Hal R. (1992): Microeconomic Analysis. New York: Norton
Wikimedia Foundation.
