Abstiegsfunktion — Eine Abstiegsfunktion ist in der Mathematik und in der Informatik eine Funktion, mit der nachgewiesen werden kann, dass eine Rekursion terminiert. Inhaltsverzeichnis 1 Prinzip 2 Beispiele 2.1 Mathematik … Deutsch Wikipedia
Mostowski-Kollaps — Der Mostowski Kollaps (auch: Mostowski scher Isomorphiesatz) ist ein Satz aus der Mengenlehre, der zuerst 1949 von dem polnischen Mathematiker Andrzej Mostowski formuliert wurde. Er ist vor allem bei der Konstruktion von Modellen ein wichtiges… … Deutsch Wikipedia
Sonja Kehler — (* 1933) ist eine deutsche Schauspielerin und Diseuse, die durch ihre Brecht Interpretationen internationale Bekanntheit erlangte. Inhaltsverzeichnis 1 Leben 2 Diskographie 3 Bühnenauftritte … Deutsch Wikipedia
Wohlfundierte Relation — In der Mathematik heißt eine auf einer Menge M definierte zweistellige Relation R wohlfundiert, wenn es keine unendlichen Ketten in dieser Relation gibt, d. h. wenn es keine unendliche Folge von Elementen in M mit für alle i gibt.… … Deutsch Wikipedia
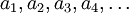 von Elementen in M mit
von Elementen in M mit 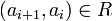 für alle i gibt. Insbesondere enthält eine wohlfundierte Relation keine Zyklen.
für alle i gibt. Insbesondere enthält eine wohlfundierte Relation keine Zyklen.