Wölbung (Statistik)

Die Wölbung oder Kurtosis (griechisch κύρτωσης kyrtōsis‚ das Krümmen, Wölben) ist eine Maßzahl für die Steilheit bzw. „Spitzigkeit“ einer (eingipfligen) Wahrscheinlichkeitsfunktion, statistischen Dichtefunktion oder Häufigkeitsverteilung.^[1] Verteilungen mit geringer Wölbung streuen relativ gleichmäßig; bei Verteilungen mit hoher Wölbung resultiert die Streuung mehr aus extremen, aber seltenen Ereignissen.

Der Exzess gibt die Differenz der Wölbung der betrachteten Funktion zur Wölbung der Dichtefunktion einer normalverteilten Zufallsgröße an.^[1]

Wölbung

Die Wölbung bzw. Kurtosis der Dichtefunktion bzw. Wahrscheinlichkeitsfunktion einer Zufallsvariablen X ist definiert als ihr auf die vierte Potenz der Standardabweichung σ normiertes viertes zentrales Moment μ₄(X).

$\beta_2=\frac{\mu_4(X)}{\mu_2(X)^2}=\frac{\mu_4(X)}{\sigma^4(X)}$.

Nicht selten wird der Exzess einer Dichtefunktion (fälschlicherweise) als ihre Wölbung oder ihre Kurtosis bezeichnet.

Exzess

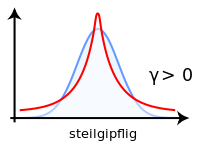
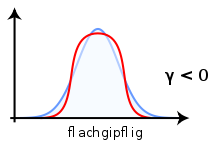
Um das Ausmaß der Wölbung einer Dichte- bzw. Wahrscheinlichkeitsfunktion besser einschätzen zu können, wird sie mit der Wölbung der Dichtefunktion einer Normalverteilung verglichen, für die μ₄(X) / σ⁴(X) = 3 gilt.

Der Exzess bzw. die Überkurtosis der Dichte- bzw. Wahrscheinlichkeitsfunktion einer Zufallsvariablen X ist daher definiert als

$\gamma_2= \beta_2 - 3 = \frac{\mu_4(X)}{\sigma^4(X)} - 3$,

wobei 3 der Wölbung der Dichtefunktion einer normalverteilten Zufallsgröße entspricht. Der Exzess einer normalverteilten Zufallsvariablen ist dementsprechend immer Null.

Alternativ kann der Exzess über die normierte vierte Kumulante

$\gamma_2 = \frac{\kappa_4(X)}{\sigma^4(X)}$

definiert werden.

Arten von Exzess

Verteilungen werden entsprechend ihres Exzesses eingeteilt in:

• γ₂ = 0: normalgipflig oder mesokurtisch. Die Normalverteilung hat die Kurtosis β₂ = 3 und entsprechend den Exzess γ₂ = 0.
• γ₂ > 0: steilgipflig, supergaußförmig oder leptokurtisch. Es handelt sich hierbei um im Vergleich zur Normalverteilung spitzere Verteilungen, d.h. Verteilungen mit starken Peaks.
• γ₂ < 0: flachgipflig, subgaußförmig oder platykurtisch. Man spricht von einer im Vergleich zur Normalverteilung abgeflachten Verteilung.

Empirische Kurtosis

Zur Berechnung der Kurtosis einer (eingipfligen) empirischen Häufigkeitsverteilung von n Beobachtungen müssen Mittelwert und Standardabweichung geschätzt werden, d.h. die theoretischen durch die empirischen Momente ersetzt werden:

$\hat{\beta}_2 = \frac{\hat{\mu}_4(x)}{\hat{\sigma}^4(x)} = \frac{\tfrac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^4}{\left(\tfrac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2\right)^2}$

mit

n der Stichprobenumfang (Anzahl der Beobachtungen)

k die Anzahl der (möglichen) Beobachtungswerte

$x_i\,$ die i-te Beobachtung

$\overline{x}$ der Stichprobenmittelwert

$\hat{\mu}_4(x)$ das aus der Stichprobe geschätze vierte zentrale Moment

$\hat{\sigma}^4(x)$ die aus der Stichprobe geschätze quadrierte Varianz, die dem quadrierten zweiten zentralen Moment entspricht

Der empirische Exzess berechnet sich damit als

$\hat{\gamma}_2 = \hat{\beta}_2 - 3.$

Siehe auch

• Moment (Stochastik), Erwartungswert, Varianz, Schiefe (Statistik)
• Krümmungsradius

Einzelnachweise

1. ↑ ^{a b} Bernd Rönz, Hans G. Strohe (1994), Lexikon Statistik, Gabler Verlag, S. 323-324