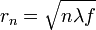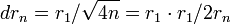Zonenlinse

Binäres Ringmuster einer Fresnel-Zonenplatte

Kosinusförmiges Ringmuster einer Fresnel-Zonenplatte

Eine Fresnel-Zonenplatte, auch Zonenlinse oder Kinoform genannt, ist eine Platte, auf der konzentrische Ringe angebracht sind. Die Zonen unterscheiden sich in ihrer Transparenz oder/und in ihrer optischen Weglänge. Im einen Fall wird die Strahlung an den ringförmigen Spalten gebeugt und durch konstruktive Interferenz in Brennpunkten verstärkt. Im anderen Fall werden die in der nebenstehenden Abbildung schwarz dargestellten Zonen durch ein transparentes Material genau bestimmter Dicke ersetzt, das eine Phasenverschiebung der Lichtwelle von 180° bewirkt, wodurch die transmittierte Strahlung dieser Zonen im Brennpunkt ebenfalls konstruktiv interferieren kann.

Außer für Licht werden Zonenplatten für die Abbildung von Röntgenstrahlung eingesetzt, da Röntgenlinsen in der konventionellen Linsenform sehr ineffizient wären.

Die Fresnel-Zonenlinse hat mit einer Fresnellinse lediglich den Erfinder gemeinsam. Beide wurden von Augustin-Jean Fresnel entwickelt.

In einer Zonenplatte mit binärer Abstufung, also völlig transparent abwechselnd mit total absorbierend (oberes Bild), wird das einfallende Licht auf viele reelle und virtuelle Brennpunkte verteilt (s. u.). Um das Licht auf die beiden Brennpunkte 1. Ordnung zu konzentrieren, ist nur ein sinusförmiger Kontrastwechsel erforderlich (unteres Bild). Die entsprechende Linse ähnelt dem Beugungsbild einer Kreisscheibe. Unterschiede in den Abständen der Maxima resultieren aus der unterschiedlichen Abbildungsweise: Dort liegt sogenannte Fraunhofer-Beugung mit Strahlung aus dem Unendlichen (die durch Linsen fokussiert wird) vor, hier so genannte Fresnel-Beugung.

Berechnung der Zonen

Für eine konstruktive Interferenz in einem Fokus müssen die Radien der abwechselnd transparenten und absorbierenden Zonen in der "quadratischen Näherung" folgender Gleichung genügen:

$r_{n} = \sqrt{n \lambda \frac{f \cdot g}{f + g}}$

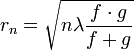
mit n = 1, 2, 3, ...; λ = Wellenlänge der Strahlung, z. B. 500 nm für Licht, 5 nm für Röntgenstrahlung; f = Bildweite, der Abstand vom Zentrum der Zonenplatte zum Bild (Fokus); g = Gegenstandsweite.

Für g >> f gilt:

$r_{n} = \sqrt{n \lambda f}$

und für die Breite der schmalsten, der äußersten Zone gilt

$dr_{n} = r_{1}/ \sqrt{ {4n}} = r_{1} \cdot r_{1}/ { 2r_{n}}$

Diese Breite entspricht - bis auf einen Faktor 1.22 - der erreichbaren räumlichen Auflösung mit einer Zoneplatte in der Mikroskopie, wenn sie in ihrer ersten Beugungsordnung benutzt wird. Man sieht hier, dass die mit einer Zonenplatte erreichbare Auflösung nicht von der Wellenlänge abhängt. 2008 betrugen die kleinsten Zonenbreiten in der Röntgenmikroskopie genutzter Mikrozonenplatten rund 0.02 µm. Bei Benutzung der Zonenplatte in ihrer m.ten Beugungsordnung ist die erreichbare Auflösung aber nochmals um den Faktor m höher. Diese Aussagen zur Auflösung sind gültig, solange die sich so ergebende rechnerische Auflösung nicht kleiner als die Wellenlänge der benutzten Strahlung ist.

Man sieht außerdem: die Breite dr_n der äußersten Zone sinkt linear mit dem Durchmesser 2r_n der Zonenplatte. Da die Länge der Zonen aber linear mit dem Durchmesser 2r_n steigt, ist die Fläche der Zonen konstant - solange die oben erwähnte quadratische Näherung gilt.

Für unendlich große Zonenzahlen n gelten diese Beziehungen zum Zonenradius und zur Zonenbreite nicht. Die Zonenbreite strebt dann gegen eine konstante Breite. Für g = f beträgt diese kleinste erreichbare Zonenbreite λ / 4.

Beispiel

Ein grün leuchtender Gegenstand (λ = 500 nm) in großer Entfernung (g ≫ f) soll von einer Zonenplatte abgebildet werden, deren innerer Radius = 10 mm (n = 1) beträgt. Für m = 1 liegt der erste Brennpunkt bei 50 m (Abstand Platte–Bild), für m = 2 bei 25 m, für m = 3 bei 17 m. Ist die Zonenplatte um eine Größenordnung kleiner ( innerer Radius 1 mm), sind die Brennweiten um 2 Größenordnungen kleiner, im Beispiel bei 0,5 m, 0,25 m usw.

Anwendung

Zonenplatten werden in der Röntgenoptik, speziell in der Röntgenmikroskopie, zur Fokussierung benutzt, da es für den Frequenzbereich mit Wellenlängen oberhalb von etwa 0,5 nm Wellenlänge keine Sammellinsen gibt, denn die Absorption in ihnen ist zu groß. Für Röntgenstrahlung ist die Brechzahl aller durchstrahlbaren Materialien minimal kleiner als 1, so dass eine einzelne Sammellinsen (bikonkav) nur minimale Fokussierung zeigt. Insbesondere unterhalb 0,1 nm Wellenlänge ist die Absorption aber so gering, dass durch eine Reihe dünnster hintereinandergeschalteter Sammellinsen doch eine experimentell nutzbare Fokussierung gelingt, mit sogenannten "compound refractive lenses".

Das Loch einer Camera obscura kann als innerer Teil einer Zonenplatte der Ordnung m = 1 aufgefasst werden.

Messung der Rauigkeit einer Oberfläche (Abstandsmessung) siehe Konoskopische Holografie

Bedeutung in der Holografie

Die Fresnel-Zonenplatte war nach ihrer Erfindung eigentlich nur ein physikalisches Kuriosum und auch noch ohne Anwendung. Doch mit der Erfindung der Holografie im Jahre 1948 kam der Zonenplatte eine ganz neue Bedeutung zu. Die Fresnelplatte entspricht nämlich weitgehend dem Hologramm eines einzelnen Bildpunktes, wenn als Referenzwelle während der Hologrammerzeugung eine Planwelle oder ebenfalls eine Kugelwelle genutzt wird. Der einzige Unterschied liegt darin, dass beim Hologramm, im Unterschied zur rechts abgebildeten Amplituden-Zonenplatte, die nur transparente und absorbierende Zonen besitzt, kontinuierliche und keine sprunghaften Transmissionübergänge vorliegen.

Der Zusammenhang wird auch klar, wenn man bedenkt, dass die Fresnel-Platte gleichzeitig als Zerstreuungslinse und als Sammellinse wirkt, d. h. sie besitzt virtuelle und reelle Brennpunkte – wie ein Hologramm, das immer reelle und konjugierte Bilder rekonstruiert, wenn es mit der zur Hologramm-Aufzeichnung benutzten Referenzwelle beleuchtet wird.

Da komplexe Objekte nichts weiter als Ansammlungen von Bildpunkten sind kann man die Interferenzmuster als Überlagerungen von sehr vielen Fresnel-Zonenplatten verstehen.

Weblinks

• Beispiele von Zonenplattenfotografie