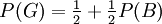Zweizettelspiel

Das Zwei-Zettel-Spiel oder auch Zwei-Umschläge-Problem optimiert die Wahrscheinlichkeit, die größere von zwei Zahlen zu finden, von denen nichts bekannt ist, außer dass sie verschieden sind.

Inhaltsverzeichnis

1 Problem
2 Strategie
3 Lösung
4 Anwendbarkeit in der Praxis
5 Verwandte Themen
- 5.1 Zwei-Zettel-Spiel und Umtauschparadoxon
- 5.2 Andere verwandte Themen
6 Literatur
7 Weblinks

Problem

In der von Thomas M. Cover (1987) aufgestellten Formulierung lautet es: Spieler 1 schreibt zwei beliebige, verschiedene Zahlen auf Zettel. Spieler 2 wählt zufällig einen davon aus, wobei beide Zettel gleich wahrscheinlich sind, und sieht sich die Zahl an. Spieler 2 muss nun entscheiden, ob die gewählte Zahl die größere ist. Die Wahrscheinlichkeit ist $P = 1 / 2$ , besser scheint es nicht zu gehen.

Ein praktisches Beispiel ist das des Hausverkaufs mit zwei Interessenten, wobei man bei Ablehnung des Angebotes nicht mehr auf den Interessenten zurückkommen kann. Insofern erinnert die Problemstellung ein wenig an das Sekretärinnenproblem mit der Problemgröße $n = 2$ . Weitere Möglichkeiten im täglichen Leben sind ein Sonderangebot im Supermarkt, eine Wohnung, eine Arbeitsstelle, der Partner fürs Leben etc. Stets steht man vor dem Dilemma, sich für oder gegen eine Alternative entscheiden zu müssen, ohne zu wissen, ob nicht noch eine bessere Gelegenheit kommt.

Strategie

Bestimme eine (beliebige, zufällige und von den anderen beiden Zahlen unabhängige) dritte Zahl Z nach irgendeiner Wahrscheinlichkeitsverteilung, deren Dichte auf den reellen Zahlen nirgends verschwindet, also z. B. einer Normalverteilung, und wähle die bekannte erste Zahl X (erstes Angebot), falls X größer ist als Z, ansonsten wähle die unbekannte zweite Zahl Y (zweites Angebot).

Lösung

Es sei X die zuerst gewählte Zahl (erstes Angebot), Y die unbekannte zweite Zahl (zweites Angebot).

Dann können drei Fälle eintreten:

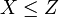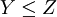Fall A: $X \leq Z$ und $Y \leq Z$ , also ist $Z$ größer sowohl als $X$ als auch $Y$ , oder höchstens gleichgroß.; Dann fällt die Wahl wegen 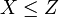$X \leq Z$ auf $Y$ .

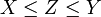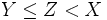Fall B: $X \leq Z \leq Y$ oder $Y \leq Z &lt; X$ , also liegt Z zwischen X und Y (einschließlich).; Dann fällt für 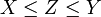$X \leq Z \leq Y$ die Wahl auf Y, für 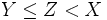$Y \leq Z &lt; X$ auf X.

Fall C: $X > Z$ und $Y > Z$ , also ist Z sowohl kleiner als X als auch Y.; Dann fällt die Wahl wegen $X > Z$ auf $X$ .

In den Fällen A und C trifft man letztlich eine Zufallswahl und die Wahrscheinlichkeit, die größere der beiden Zahlen $X$ oder $Y$ zu wählen, ist gleich 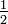$\tfrac{1}{2}$ . Im Fall B wählt man mit Sicherheit, also mit der Wahrscheinlichkeit 1, die größere der beiden Zahlen.

Vorausgesetzt, die Fälle A, B und C mit ihren Wahrscheinlichkeiten $P (A)$ , $P (B)$ und $P (C)$ sind von der Wahl von Z unabhängig, ergibt sich die Wahrscheinlichkeit, die größte Zahl zu treffen $P (G)$ aus:

$P(G)=\tfrac{1}{2}\ P(A)+1\ P(B)+\tfrac{1}{2}\ P(C)=\tfrac{1}{2}\left[P(A)+P(B)+P(C)\right]+\tfrac{1}{2}P(B)$

Da einer der Fälle A, B oder C eintreten muss, ist $P (A) + P (B) + P (C) = 1$ . Für die Gesamtwahrscheinlichkeit folgt

$P(G)=\tfrac{1}{2} + \tfrac{1}{2}P(B)$

$P (G)$ ist somit größer als 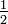$\tfrac{1}{2}$ , falls 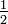$\tfrac{1}{2}$ $P (B)$ größer als Null ist. Somit ergibt sich durch die Verfolgung der oben erläuterten Strategie eine Erhöhung der Wahrscheinlichkeit, die größere Zahl zu wählen, über 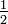$\tfrac{1}{2}$ hinaus.

Anwendbarkeit in der Praxis

Die oben genannte Lösungsstrategie beruht letztlich nur auf zwei Annahmen:

Es muss sichergestellt werden, dass 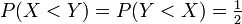$P(X &lt; Y) = P(Y &lt; X) = \tfrac 12$ gilt.
Die Zufallsvariable Z muss eine Dichtefunktion besitzen, die auf der gesamten reellen Achse positiv ist.

Sofern die erste Voraussetzung erfüllt ist, stellt sich somit die Frage, wie man Z optimal wählt.

P(G), die Wahrscheinlichkeit, die größere der beiden Zahlen zu treffen, wird dann maximal, wenn P(B) maximal wird, also die Wahrscheinlichkeit, ein Z zu finden, das zwischen X und Y liegt. Das theoretische Maximum P(B)=1 lässt sich aber nicht erreichen, da die Dichtefunktion von Z nirgends verschwinden darf. Für die genaue Wahl der Verteilung von Z lassen sich keine allgemeinen Regeln angeben, eine gute Wahl hängt von der konkreten Situation ab.

Beim Eingangsbeispiel des Hauskaufs beispielsweise gibt es eine Spannbreite, innerhalb derer die Zahlen sinnvoll erscheinen, allerdings sind - bei einem normalen Haus - beispielsweise Zahlen von kleiner als 10.000 oder von größer als 10 Millionen äußerst unwahrscheinlich. Sinnvollerweise sollte man den Erwartungswert von Z in der Nähe des Marktwerts des Hauses ansiedeln; die Varianz von Z sollte man umso kleiner wählen, je genauer man den Marktwert abschätzen kann.

Je nach Vorwissen kann eine andere Strategie als das Zwei-Zettel-Spiel zweckmäßiger sein, beispielsweise bei einem Einkauf im Supermarkt: Wenn eine Kundin erkennt, dass ein Produkt zu einem Preis angeboten wird, der nie zuvor unterboten worden ist, wird sie die Wahrscheinlichkeit, dass dieses Produkt in einem anderen Laden günstiger angeboten wird, als sehr gering einschätzen, eine Anwendung des Zwei-Zettel-Spieles wäre widersinnig. Ein Kunde hingegen, der dieses Produkt noch nie gekauft hat, und der auch sonst keine Vorinformationen hat, kann sehr wohl nach der Methode des Zwei-Zettel-Spieles vorgehen.

Literatur

F. Thomas Bruss: Der Ungewissheit ein Schnippchen schlagen. In: Spektrum der Wissenschaft. 06/2000. Spektrum der Wissenschaft Verlagsgesellschaft, S. 106
Cover, T. (1987): Open Problems in Communication and Computation. Problem 5.1: Pick the largest number. Springer Verlag, New York. (englisch). ISBN 3540966218

Weblinks

http://www.wissenschaft-online.de/abo/spektrum/archiv/4947

Wikimedia Foundation.

Игры ⚽ Нужна курсовая?