Wahrscheinlichkeitsverteilung

In der Wahrscheinlichkeitstheorie gibt die Wahrscheinlichkeitsverteilung an, wie sich die Wahrscheinlichkeiten auf die möglichen Zufallsergebnisse, insbesondere die möglichen Werte einer Zufallsvariablen, verteilen.

Die Wahrscheinlichkeitsverteilung erfasst den Zufall in einem stochastischen Vorgang quantitativ und stellt das theoretische Pendant zur empirischen Häufigkeitsverteilung dar, die sich aus der Analyse von Daten (Messwerten) ergibt.

Man unterscheidet zwischen diskreten Verteilungen, die sich auf eine endliche oder abzählbare Menge konzentrieren, und stetigen (kontinuierlichen) Verteilungen, die sich auf größere Bereiche erstrecken und bei denen einzelne Punkte die Wahrscheinlichkeit 0 haben. Beispiele für diskrete Verteilungen sind die Binomialverteilung und die Hypergeometrische Verteilung, die die Anzahl der Erfolge beim Ziehen aus einer Urne mit und ohne Zurücklegen beschreiben, sowie die Poisson-Verteilung, die sich aus der Binomialverteilung ergibt, wenn man die Erfolgswahrscheinlichkeit immer weiter reduziert und gleichzeitig die Anzahl der Ziehungen um denselben Faktor erhöht. Ein prototypischer Vertreter von stetigen Verteilungen, durch den sich viele reale Situationen approximativ beschreiben lassen und der nützliche mathematische Eigenschaften hat, ist die Normalverteilung, bei der die Wahrscheinlichkeiten einer Gaußschen Glockenkurve folgen.

Eigenschaften, welche sich allein über gemeinsame Verteilungen von Zufallsvariablen ausdrücken lassen, werden auch wahrscheinlichkeitstheoretisch genannt. Für Behandlung solcher Eigenschaften ist es nicht notwendig, die konkrete Gestalt des (Hintergrund-)Wahrscheinlichkeitsraumes zu kennen, auf dem die Zufallsvariablen definiert sind. Wichtige wahrscheinlichkeitstheoretische Eigenschaften sind der Erwartungswert und die stochastische Unabhängigkeit.^[1]

Beschreibung von Wahrscheinlichkeitsverteilungen

Zur Beschreibung von Wahrscheinlichkeitsverteilungen werden unter anderem Wahrscheinlichkeitsfunktionen, Dichtefunktionen, Verteilungsfunktionen und Wahrscheinlichkeitsmaße verwendet.

Der mathematisch allgemeinste Begriff, der nicht nur diskrete und stetige Verteilungen, sondern auch Mischungen von solchen umfasst und für beliebige Ergebnismengen Gültigkeit besitzt, ist das Wahrscheinlichkeitsmaß, d. h. eine Funktion μ, die jedem Ereignis A eine Wahrscheinlichkeit μ(A) zuordnet. In der Wahrscheinlichkeitstheorie versteht man unter der Verteilung einer Zufallsvariable X das Wahrscheinlichkeitsmaß $\mu(A) = P(X\in A)$, welches die Wahrscheinlichkeiten erfasst, mit denen die Zufallsvariable bestimmte Werte annimmt (Bildmaß von X).

Diskrete Verteilungen lassen sich durch eine Wahrscheinlichkeitsfunktion (oder Zähldichte) ρ(x) beschreiben, die die Wahrscheinlichkeiten für die einzelnen Werte x angibt. Der Zusammenhang zum Wahrscheinlichkeitsmaß ergibt sich aus ρ(x) = μ({x}) bzw. ρ(x) = P(X = x). Die Wahrscheinlichkeiten für beliebige Ereignisse A erhält man als Summen:

$P(X \in A) \, = \, \sum_{x\in A} \rho(x)$    bzw.    $\mu(A) \, = \, \sum_{x\in A} \rho(x)$

Bei stetigen Verteilungen lassen sich Wahrscheinlichkeiten nicht als Summen von Einzelwahrscheinlichkeiten berechnen, da für stetige Zufallsvariablen X stets P(X = x) = 0 gilt. Sie lassen sich jedoch oft als Integrale über eine Dichtefunktion (oder Wahrscheinlichkeitsdichte) f(x) darstellen (stetige Verteilungen im engeren Sinne):

$P(a \le X \le b) \, = \, \int_a^b f(x)\,dx$    bzw.    $\; \mu([a,b]) \, = \, \int_a^b f(x)\,dx$

Verteilungen auf den reellen Zahlen können allgemein durch die (kumulative) Verteilungsfunktion (engl. cumulative distribution function, cdf) F(x) beschrieben werden, die angibt, mit welcher Wahrscheinlichkeit die Zufallsvariable einen Wert kleiner oder gleich x annimmt:

$F(x) \, = \, P(X \le x)$

bzw.

$F(x) \, = \, \mu\left(]-\infty, x]\right)$

Wenn die Verteilungsfunktion differenzierbar ist, ist ihre Ableitung eine Dichtefunktion der Verteilung.

Wichtige stetige Wahrscheinlichkeitsverteilungen

Drei Glockenkurven (Dichtefunktion normalverteilter Zufallsgrößen)

Dichten verschiedener beta-verteilter Zufallsgrößen

Dichtefunktion der F-Verteilung mit ausgewählten Freiheitsgraden m und n

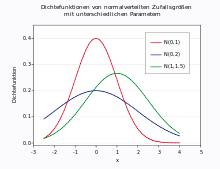
Die meisten Wahrscheinlichkeitsverteilungen lassen sich bei großer Stichprobe zur Normalverteilung überleiten. Viele natur-, wirtschafts- und ingenieurswissenschaftliche Vorgänge lassen sich durch die Normalverteilung entweder exakt oder wenigstens in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).

Die Chi-Quadrat-Verteilung ist eine so genannte Stichprobenverteilung, die bei der Schätzung von Verteilungsparametern, beispielsweise der Varianz, Anwendung findet.

Über der gesamten Zahlengeraden:

• Normalverteilung (Gauß-Verteilung, Glockenkurve, siehe Bild)
• Cauchy-Verteilung (Lorentz-Verteilung)
• Crystal-Ball-Funktion
• Extremwertverteilung
• Fisher-Tippett-Verteilung
• Fishersche z-Verteilung
• Gumbel-Verteilung
• Laplace-Verteilung (Doppelexponentialverteilung)
• Lévy-Verteilung
• Logistische Verteilung
• Rayleigh-Verteilung
• Rossi-Verteilung
• Studentsche t-Verteilung

Für konvexe Kombinationen mehrerer Verteilungen siehe Mischverteilung, dessen Sonderfall

• Kontaminierte Normalverteilung

darstellt.

Über einem endlichen Intervall [a,b], im einfachsten Fall [0,1]:

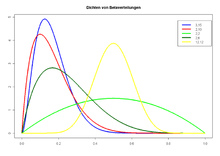
• Betaverteilung (siehe Bild)
• Dreiecksverteilung (Simpson-Verteilung)
• Stetige Gleichverteilung (Rechteck- oder Uniformverteilung)

Über einem halbseitig unendlichen Intervall, üblicherweise als [0,∞] angenommen:

• χ²-Verteilung
• Erlang-Verteilung
• Exponentialverteilung
• F-Verteilung (siehe Bild)
• Gammaverteilung
• Inverse Normalverteilung (Inverse Gauß-Verteilung, Wald-Verteilung)
• Logarithmische Gammaverteilung
• Logarithmische Normalverteilung
• Pareto-Verteilung, Verschobene Pareto-Verteilung
• Weibull-Verteilung

Verteilungsklassen

Verteilungsklasse oder Verteilungsfamilie bezeichnet Verteilungen gleichen Typs. Man unterscheidet sie anhand unterschiedlicher mathematischer Eigenschaften. Man unterscheidet parametrische Klassen und nicht-parametrische Klassen. Zur Klasse der parametrischen Klassen gehört die Exponentielle Familie. Sie vereinigt:

• Normalverteilung
• Binomialverteilung
• Multinomialverteilung
• Poisson-Verteilung
• Gammaverteilung
• Inverse Normalverteilung

Die Familie der Beta-Verteilungen wird "die zur Binomial-Verteilung “konjugierte” Verteilungsklasse" genannt. Die Panjer-Verteilung vereint Negative Binomialverteilung, Binomialverteilung und Poisson-Verteilung in einer Verteilungsklasse. Man sondiert auch die Verteilungsfamilie mit einem monotonen Dichtequotienten, die Dominierte Verteilungsfamilie, und Alpha-stabile Verteilungen auf Grund von unterschiedlichen Gesichtspunkten.

Siehe auch

• Liste univariater Wahrscheinlichkeitsverteilungen
• Alpha-stabile Verteilungen; Näherungslösungen für diskrete Verteilungen
• Heavy-tailed-Verteilung
• Boltzmann-Verteilung

Literatur

• Erich Härtter: Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Vandenhoeck & Ruprecht, Göttingen 1974, ISBN 3-525-03114-9

Einzelnachweise

1. ↑ Heinz Bauer: Wahrscheinlichkeitstheorie. De Gruyter, Berlin 2002, ISBN 3-11-017236-4, S. 15.

Weblinks

 Wikibooks: Einführung in Zufallsvariablen – Lern- und Lehrmaterialien

• Interaktive graphische Darstellungen verschiedener Wahrscheinlichkeitsfunktionen bzw. Dichten (Uni Konstanz)
• Katalog der Wahrscheinlichkeitsverteilungen in der Gnu Scientific Library.
• Numerische Berechnung und Darstellung von Dichten und Verteilungsfunktionen einiger wichtiger Wahrscheinlichkeitsverteilungen
• Weitere Verteilungen aus dem Wiki der Uni Frankfurt