- Berechnung elektrostatischer Felder
-
Grundlage für die Berechnung des elektrostatischen Feldes in der Umgebung einfacher geometrischer Körper wie Platte, Linienladung oder Kugel ist das gaußsche Gesetz. Man legt um die vorgegebene Ladungsverteilung eine möglichst einfache, geschlossene Hüllfläche aus wenigen Flächenelementen, für die der Fluss Φ leicht bestimmt werden kann.
Inhaltsverzeichnis
Konfigurationen
Punktladung
Eine elektrisch geladene Kugel (Ladung Q) ist von Feldstärkevektoren E umgeben, die radial nach außen laufen. Keine Richtung wird bevorzugt. Als geschlossene Hüllfläche im Sinne des gaußschen Gesetzes legt man darum eine konzentrische Kugel mit dem Radius R, die von den Feldstärkevektoren lotrecht durchstoßen wird.
Die Hüllfläche mit der Fläche 4π·R² denkt man sich aus vielen winzigen Quadraten zusammengesetzt. Jedes besitzt eine Flächennormale dA, die exakt parallel zum durchtretenden Vektor der Feldstärke ist. Deshalb besitzt jedes Skalarprodukt den Wert dA·E. Summiert man alle Produkte, erhält man das Resultat
Das gaußsche Gesetz fordert auch:
Ein Vergleich der rechten Seiten liefert das Ergebnis
Bei doppeltem Abstand sinkt die Feldstärke auf ein Viertel.
Linienladung
Ein elektrisch geladener, unendlicher langer Draht trage pro Längeneinheit die Ladung Q. Das entspricht der Ladungsdichte λ = Q/L.
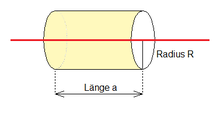
Aus Symmetriegründen bilden die Vektoren E der elektrischen Feldstärke rechte Winkel mit dem Draht und durchstoßen die gelb eingezeichnete Zylinderwand senkrecht. Würde man diese Vektoren einzeichnen, ergäbe sich das Bild einer Rundbürste, wie sie zur Reinigung von Flaschen oder Gewehrläufen verwendet wird.
Als geschlossene Hüllfläche im Sinne des gaußschen Gesetzes legt man um einen Abschnitt dieses Drahtes einen geraden Kreiszylinder der Länge a, der den Draht als Achse besitzt. Die Hüllfläche besteht aus drei Elementen:
- Linker und rechter Deckel mit den Flächen π·R²; jede Flächennormale ist parallel zum Draht und bildet deshalb mit den radial verlaufenden Vektoren der Feldstärke rechte Winkel. Dieser sorgt wiederum dafür, dass die entsprechenden Skalarprodukte unabhängig von der Größe der Deckel den Wert Null besitzen und keinen Beitrag zum Fluss-Integral liefern.
- Zylinderwand mit der Fläche 2π·R·a, die man sich aus vielen winzigen Quadraten zusammengesetzt denkt. Jedes besitzt eine Flächennormale dA, die exakt parallel zum durchtretenden Vektor der Feldstärke ist. Deshalb besitzt jedes Skalarprodukt den Wert dA·E. Summiert man alle Produkte, erhält man das Resultat
Andererseits muss gelten:
Ein Vergleich der rechten Seiten liefert das Ergebnis
Bei doppelter Entfernung sinkt die Feldstärke auf die Hälfte. Der Draht muss nicht tatsächlich unendlich lang sein. Es genügt, wenn der Abstand R, in dem die Feldstärke gemessen wird, viel kleiner ist als die Drahtlänge. Andernfalls treten Randeffekte auf und der Anteil von Boden und Deckel muss mit berücksichtigt werden.
Flächenladung
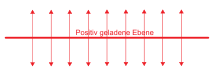
Eine positiv geladene, unendliche große Ebene trage pro Flächeneinheit die Ladung Q. Das entspricht der Ladungsdichte σ = Q/A.
Aus Symmetriegründen stehen die Vektoren E der elektrischen Feldstärke lotrecht auf der Ebene. Würde man alle Vektoren einzeichnen, ergäbe sich das Bild einer Doppel-Bürste, die sowohl oben als auch unten Borsten besitzt.
Als geschlossene Hüllfläche im Sinne des gaußschen Gesetzes legt man um eine Teilfläche einen Quader der Höhe 2·H, der von der geladenen Ebene etwa halbiert wird. Die E-Vektoren durchstoßen beide Deckel des Quaders senkrecht.Seine Oberfläche besteht aus drei Elementen:
- Oberer und unterer Deckel mit den Flächen A; jede Flächennormale steht senkrecht zur geladenen Ebene und ist deshalb parallel zur Feldstärke E. Durch jeden der beiden Deckel geht der Fluss Φoben = Φunten = A·E nach außen.
- Der Rand des Quaders trägt nichts bei zum Fluss Φ, weil E mit den jeweiligen Flächennormalen rechte Winkel einschließt. Daran hätte sich auch nichts geändert, wenn man statt des Quaders ein Prisma mit anderer Grundfläche oder einen Zylinder gewählt hätte. Auch die Höhe H ist ohne Belang.
Der Gesamtfluss beträgt also
Wegen der im Quader enthaltenen Ladung gilt
Ein Vergleich der rechten Seiten liefert das Ergebnis
Die Feldstärke E ist also unabhängig vom Abstand H zur (unendlich ausgedehnten) geladenen Ebene. Wenn die Ebene begrenzt ist, gilt dieses Ergebnis nur für hinreichend geringe Abstände.
Zwei entgegengesetzt geladene Flächenladungen
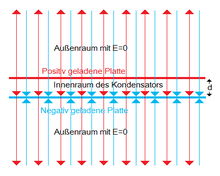
Eine positiv geladene, sehr große Ebene trage pro Flächeneinheit die Ladung Q. Das entspricht der Ladungsdichte σ = Q/A. Im Abstand d verläuft eine parallele Ebene der Ladungsdichte -σ. Diese Anordnung wird auch als Plattenkondensator bezeichnet. Um Polaritäten unterscheiden zu können, wurde vereinbart, dass die Feldlinien von der positiven Platte weg zeigen (rot eingezeichnet) und zur negativen Platte hin zeigen (blau eingezeichnet).
Zwischen den beiden Platten sind die Pfeile gleich orientiert, dort addieren sich die einzelnen Feldstärken zu
Im Außenraum sind die Pfeile entgegengesetzt gerichtet, dort kompensieren sich die Feldstärken und es gilt Egesamt = 0. Vereinfachend sagt man, das elektrische Feld ist nur im Innenraum eines Kondensators vorhanden.
Wikimedia Foundation.