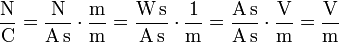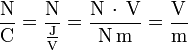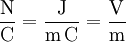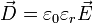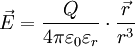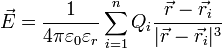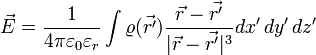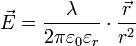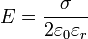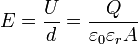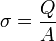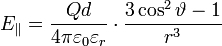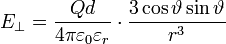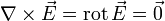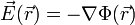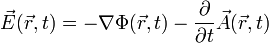- E-Feld
-
Physikalische Größe Name Elektrische Feldstärke Formelzeichen der Größe E Größen- und
Einheiten-
systemEinheit Dimension SI V·m-1 M·L·I-1·T-3 Der Begriff des elektrischen Feldes bezeichnet in der Elektrostatik und in der Elektrodynamik einen Zustand des Raumes, der
- von den vorhandenen elektrischen Ladungen und
- von der zeitlichen Änderung des magnetischen Feldes
verursacht wird. Das elektrische Feld ist ein Vektorfeld: Jedem Punkt des Raumes wird gemäß der Definition weiter unten ein Vektor zugeordnet, nämlich die elektrische Feldstärke
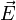 . Veranschaulichen lassen sich elektrische Felder durch Feldlinienbilder.
. Veranschaulichen lassen sich elektrische Felder durch Feldlinienbilder.Ladungen werden vom elektrischen Feld beeinflusst: Auf eine Ladung q, an deren Position der Feldstärkevektor gleich
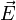 ist, wirkt die Kraft
ist, wirkt die Kraft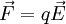 .
.
Durch Änderungen des elektrischen Feldes werden magnetische Wirbelfelder erzeugt (siehe Verschiebungsstrom).
Allgemeines
Verknüpfung mit dem magnetischen Feld
Das elektrische Feld in allgemeiner Form ist sowohl orts- als auch zeitabhängig,
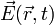 . Es ist über die maxwellschen Gleichungen und die spezielle Relativitätstheorie eng mit dem magnetischen Feld verknüpft. In der speziellen Relativitätstheorie werden seine Vektorkomponenten daher untrennbar mit denen des magnetischen Feldes zu einem Tensor zusammengefasst. Je nachdem, in welchem Bezugssystem man sich als Beobachter befindet, d. h. in welcher relativen Bewegung zu eventuell vorhandenen Raumladungen, wird so über die Lorentz-Transformation das elektrische Feld in ein magnetisches Feld transformiert und umgekehrt.
. Es ist über die maxwellschen Gleichungen und die spezielle Relativitätstheorie eng mit dem magnetischen Feld verknüpft. In der speziellen Relativitätstheorie werden seine Vektorkomponenten daher untrennbar mit denen des magnetischen Feldes zu einem Tensor zusammengefasst. Je nachdem, in welchem Bezugssystem man sich als Beobachter befindet, d. h. in welcher relativen Bewegung zu eventuell vorhandenen Raumladungen, wird so über die Lorentz-Transformation das elektrische Feld in ein magnetisches Feld transformiert und umgekehrt.Unterschiede in der Elektrostatik und der Elektrodynamik
In der Elektrostatik werden ausschließlich ruhende Ladungen betrachtet. In diesem Fall existiert kein Magnetfeld, und das elektrische Feld (auch als elektrostatisches Feld bezeichnet) ist stationär, also zeitlich unveränderlich. Ein wichtiger Sonderfall ist das homogene elektrische Feld, bei dem Richtung und Betrag der elektrischen Feldstärke in jedem Punkt gleich sind, die Feldlinien also parallele Geraden sind. Das Feld im Inneren eines Plattenkondensators ist näherungsweise homogen (siehe unten sowie Berechnung elektrostatischer Felder).
In der Elektrodynamik muss man auch elektrische Felder berücksichtigen, die durch zeitlich veränderliche Magnetfelder hervorgerufen werden (elektromagnetische Induktion). Ein besonders wichtiges Beispiel sind die elektromagnetischen Wellen wie Licht, die aus miteinander verketteten elektrischen und magnetischen Feldern bestehen. Aufgrund der engen Beziehung zwischen elektrischem und magnetischem Feld fasst man beide in der Elektrodynamik zum elektromagnetischen Feld zusammen.
Nahwirkung statt Fernwirkung
Nach dem coulombschen Gesetz übt jede Ladung auf jede andere Ladung eine abstoßende oder anziehende Kraft aus. Die naheliegende Vorstellung einer Fernwirkung zwischen den Ladungen wäre allerdings problematisch. Sie würde nämlich bedeuten, dass sich eine Veränderung der Ladungsverteilung sofort, also mit unendlicher Geschwindigkeit ausbreiten würde. Daher geht man davon aus, dass die Ladungen die Eigenschaften des umgebenden Raumes beeinflussen, und spricht von dem elektrischen Feld, das von den Ladungen verursacht wird. Durch dieses elektrische Feld wiederum werden Kräfte auf Ladungen ausgeübt. Da die Kraft vom elektrischen Feld an der betreffenden Stelle abhängt, aber nicht direkt vom elektrischen Feld an anderen Punkten, handelt es sich um eine Nahwirkung. Ändert sich die Position einer der Ladungen, die das elektrische Feld erzeugen, so breitet sich die Änderung des Feldes mit endlicher Geschwindigkeit aus, im Vakuum beispielsweise mit Lichtgeschwindigkeit.
Elektrische Feldstärke
Das elektrische Feld lässt sich durch Einführung einer vektoriellen Größe, der elektrischen Feldstärke
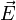 beschreiben. Diese ist in einem gegebenen Punkt definiert durch
beschreiben. Diese ist in einem gegebenen Punkt definiert durch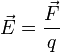 .
.
q (mit Vorzeichen!) bedeutet dabei eine kleine Probeladung, die sich am gegebenen Punkt befindet.
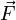 ist die auf diese Probeladung wirkende Kraft. Diese Definition ist wegen der Proportionalität von Kraft und Ladung sinnvoll.
ist die auf diese Probeladung wirkende Kraft. Diese Definition ist wegen der Proportionalität von Kraft und Ladung sinnvoll.Die SI-Einheit von
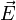 ist Newton pro Coulomb oder Volt pro Meter, denn es gilt:
ist Newton pro Coulomb oder Volt pro Meter, denn es gilt:bzw.
oder
Ebenfalls zur Beschreibung des elektrischen Feldes verwendet wird die elektrische Flussdichte (Verschiebungsdichte)
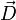 , die über die Materialgleichung
, die über die Materialgleichungmit der elektrischen Feldstärke
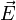 verknüpft ist.
verknüpft ist.Feldlinienbilder
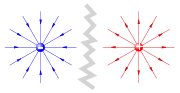
Eine anschauliche Vorstellung von elektrischen Feldern erhält man durch Feldlinienbilder. Diese bestehen aus orientierten (mit Pfeilen versehenen) Feldlinien, die jeweils von positiven Ladungen ausgehen und an negativen Ladungen enden. Die Richtung der Tangente in einem Punkt einer Feldlinie gibt die Richtung des Feldstärkevektors
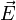 an. In der Regel werden Feldlinienbilder so gezeichnet, dass die Dichte der Feldlinien Rückschlüsse auf den Betrag der Feldstärke zulässt.
an. In der Regel werden Feldlinienbilder so gezeichnet, dass die Dichte der Feldlinien Rückschlüsse auf den Betrag der Feldstärke zulässt.Elektrisches Feld einer Punktladung
Besonders einfach zu ermitteln ist das elektrische Feld einer Punktladung. Gemäß dem coulombschen Gesetz ergibt sich für die Feldstärke in einem gegebenen Punkt:
Dabei steht Q (mit Vorzeichen!) für die felderzeugende Ladung (im Ursprung des Koordinatensystems),
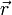 für den Ortsvektor des gegebenen Punktes,
für den Ortsvektor des gegebenen Punktes, 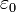 für die Permittivität des Vakuums und
für die Permittivität des Vakuums und 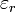 für die relative Permittivität.
für die relative Permittivität.Elektrisches Feld einer Ladungsverteilung
Wird das elektrische Feld durch mehrere Punktladungen
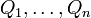 an den Positionen
an den Positionen 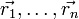 erzeugt, so erhält man den Feldstärkevektor des Gesamtfeldes an der Position
erzeugt, so erhält man den Feldstärkevektor des Gesamtfeldes an der Position 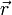 gemäß dem Superpositionsprinzip durch Addition der einzelnen Feldstärkevektoren:
gemäß dem Superpositionsprinzip durch Addition der einzelnen Feldstärkevektoren:Liegt eine kontinuierliche, durch die räumliche Ladungsdichte
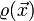 gegebene Ladungsverteilung vor, so gilt entsprechend:
gegebene Ladungsverteilung vor, so gilt entsprechend:Weitere Beispiele für elektrische Felder
Elektrisches Feld einer Linienladung
Das elektrische Feld einer Linienladung (eines unendlich langen, geladenen Drahtes) mit der linearen Ladungsdichte
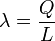 ist gegeben durch
ist gegeben durchDabei ist der Vektor
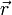 radial von der Linienladung zum Bezugspunkt gerichtet. Diese Formel kann mit Hilfe des gaußschen Gesetzes hergeleitet werden.
radial von der Linienladung zum Bezugspunkt gerichtet. Diese Formel kann mit Hilfe des gaußschen Gesetzes hergeleitet werden.Elektrisches Feld einer Flächenladung
Eine Flächenladung (eine gleichmäßig geladene, unendlich ausgedehnte, dünne Platte) erzeugt auf beiden Seiten jeweils ein homogenes elektrisches Feld. Der Feldstärkevektor ist für einen beliebigen Punkt senkrecht zur Platte und bei positiver Ladung von der Platte weg gerichtet, bei negativer Ladung zur Platte hin. Setzt man die Flächenladungsdichte
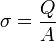 voraus, so hat die elektrische Feldstärke den Betrag
voraus, so hat die elektrische Feldstärke den BetragDiese Formel kann mit Hilfe des gaußschen Gesetzes hergeleitet werden.
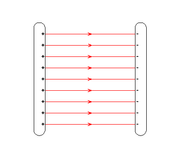
Homogenes elektrisches Feld (Plattenkondensator)
Das elektrische Feld zwischen zwei (streng genommen unendlich großen) planparallelen Kondensatorplatten, die Ladungen von gleichem Betrag, aber verschiedenem Vorzeichen enthalten, ist annähernd homogen. Für den Betrag der Feldstärke gilt:
Dabei ist d der Abstand zwischen den Platten, A die Fläche einer Kondensatorplatte, U die Spannung zwischen den beiden Platten und Q der Betrag der Ladung auf einer Platte. Außerhalb des Kondensators ist die Feldstärke (im Idealfall) gleich 0.
Die Ladungen auf den Kondensatorplatten verteilen sich dabei gleichmäßig auf den einander zugewandten Plattenflächen. Die absoluten Beträge der Flächenladungsdichte
und der elektrischen Flussdichte
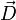 stimmen überein. Allerdings ist σ eine skalare Größe,
stimmen überein. Allerdings ist σ eine skalare Größe, 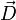 dagegen vektoriell. Die Herleitung der Formel erfolgt mit Hilfe des gaußschen Gesetzes.
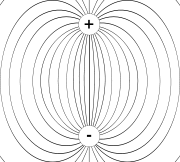
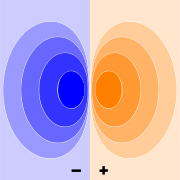
dagegen vektoriell. Die Herleitung der Formel erfolgt mit Hilfe des gaußschen Gesetzes.Elektrisches Feld eines Dipols
Ein elektrischer Dipol, also eine Anordnung aus zwei Punktladungen mit gleichem Ladungsbetrag, aber verschiedenem Vorzeichen, erzeugt ein rotationssymmetrisches Feld. Für die Feldstärkekomponenten parallel und senkrecht zur Dipolachse gilt in großem Abstand vom Dipol näherungsweise:
Dabei steht Q für den Ladungsbetrag, d für den Abstand der Ladungen. Weiter wurde vorausgesetzt, dass sich die Ladung + Q an der Stelle
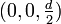 und die Ladung − Q an der Stelle
und die Ladung − Q an der Stelle 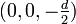 befindet. r bezeichnet den Abstand des gegebenen Punktes vom Dipolmittelpunkt,
befindet. r bezeichnet den Abstand des gegebenen Punktes vom Dipolmittelpunkt, 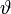 den Winkel zwischen der positiven z-Achse und der Verbindungslinie zwischen Dipolmittelpunkt und gegebenem Punkt.
den Winkel zwischen der positiven z-Achse und der Verbindungslinie zwischen Dipolmittelpunkt und gegebenem Punkt.Eigenschaften des elektrischen Feldes
Elektrostatische Felder existieren in der nichtleitenden Umgebung ruhender Ladungen, beispielsweise in der Nähe elektrisch aufgeladener Isolierstoffe. Es fließen keine Ströme. Unter dieser Voraussetzung sind elektrostatische Felder wirbelfrei, sodass die Rotation von
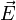 verschwindet:
verschwindet:Im Rahmen der allgemeinen Elektrodynamik gilt die Wirbelfreiheit des elektrischen Feldes nicht mehr (siehe maxwellsche Gleichungen).
Elektrostatische Felder sind Quellenfelder. Es gibt also Punkte, von denen Feldlinien in alle Richtungen ausgehen (Quellen), und Punkte, zu denen Feldlinien aus allen Richtungen hinführen (Senken). Ursache solcher Felder sind elektrische Ladungen mit der Quellendichte
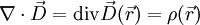 .
.
Die Energiedichte des elektrischen Feldes lässt sich berechnen durch
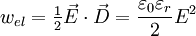 .
.
Zusammenhang mit dem Potential
In vielen Fällen lässt sich die elektrische Feldstärke am einfachsten über das zugehörige Potential berechnen. Im Rahmen der Elektrostatik ist die elektrische Feldstärke gleich dem negativen Gradienten des (skalaren) elektrischen Potentials Φ.
Die entsprechende allgemeinere Gleichung der Elektrodynamik berücksichtigt auch das Vektorpotential
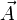 und die Zeitabhängigkeit.
und die Zeitabhängigkeit.Leiter im elektrischen Feld
Bringt man einen Leiter in ein zeitlich konstantes elektrisches Feld, so verschieben sich zufolge der Influenz die beweglichen Ladungen des Leiters (zum Beispiel Elektronen) derart, dass die elektrische Feldstärke im Inneren des Leiters gleich 0 ist. Außerhalb des Leiters ist der Feldstärkevektor an jedem Punkt der Leiteroberfläche senkrecht zu dieser.
Siehe auch
Literatur
- Adolf J. Schwab: Begriffswelt der Feldtheorie: Praxisnahe, anschauliche Einführung. Elektromagnetische Felder, Maxwellsche Gleichungen, Gradient, Rotation, Divergenz. 6. Auflage. Springer, Berlin 2002, ISBN 3-540-42018-5.
Weblinks
Wikimedia Foundation.