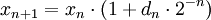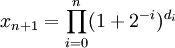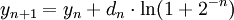- Bitalgorithmen
-
Der BKM-Algorithmus ist ein iterativer Algorithmus, mit dessen Hilfe sich die Logarithmus- und Exponentialfunktion effizient in digitalen Schaltungen berechnen lassen. Er wurde 1994 von J.C. Bajard, S. Kla, and Jean-Michel Muller entwickelt, wovon sich auch die Bezeichnung ableitet. [1]
Inhaltsverzeichnis
Allgemeines
Der BKM-Algorithmus ist wie CORDIC-Algorithmus ein so genannter Shift-And-Add-Algorithmus und basiert auf bitweisen Verschiebungen und ganzzahligen Additionen in Addierwerken. Divisionen werden ausschließlich mit negativen Potenzen von 2 durchgeführt, welche sich in digitalen Schaltungen direkt als bitweise Verschiebung implementieren lassen. Er kommt im Gegensatz zu dem CORDIC-Verfahren ohne Skalierungsfaktor aus und verwendet Logarithmentabellen anstelle der bei CORDIC notwendigen Arkustangens-Tabelle.
Die Berechnung eines Funktionswertes erfolgt in einem Iterationsverfahren mit einer Konvergenzrate von ungefähr einem Bit pro Durchlauf. Aus diesem Umstand heraus wird dieser Algorithmus manchmal auch als Bitalgorithmus bezeichnet.
Herleitung des Algorithmus
Gegeben sei die Iterationsvorschrift
mit
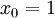 und
und 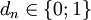 . Die Iterationsvorschrift ist identisch mit
. Die Iterationsvorschrift ist identisch mitSind alle
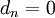 so sind alle
so sind alle 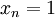 . Sind alle
. Sind alle 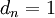 gilt
gilt 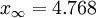 , d. h. mit der Iterationsvorschrift kann bei geeigneter Wahl der
, d. h. mit der Iterationsvorschrift kann bei geeigneter Wahl der 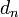 jede reelle Zahl
jede reelle Zahl 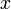 im Bereich
im Bereich 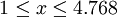 dargestellt werden.
dargestellt werden.Weiterhin gelte die Iterationsvorschrift
mit
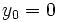
oder identisch
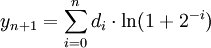
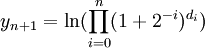 .
.
Für numerische Berechnungen wird An = ln(1 + 2 − n) durch eine voraus berechnete Tabelle realisiert.
Per Induktion folgt dann sofort, dass yn = ln(xn) für alle n gilt. Mit denselben Überlegungen wie oben ergibt sich für den Logarithmus der Bereich
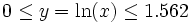 .
.Logarithmusfunktion
Um die Logarithmusfunktion zu berechnen, dies wird bei dem BKM-Algorithmus auch als L-mode bezeichnet, wird in jedem Schritt getestet, ob
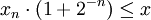 ist. Wenn ja, wird xn + 1 und yn + 1 berechnet. Nach N Schritten ist der Funktionswert mit einem Fehler
ist. Wenn ja, wird xn + 1 und yn + 1 berechnet. Nach N Schritten ist der Funktionswert mit einem Fehler 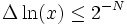 bestimmt.
bestimmt.Beispiel als C++-Programm (Tabelle A_e im Anhang):
double Logarithmus ( const double Argument, int N = 53 ) // 1 <= Argument <= 4.768462058 { double x = 1. ; double y = 0. ; double z ; double s = 1. ; int k ; for ( k = 0; k < N; k++ ) { z = x + x*s ; if ( z <= Argument ) { x = z ; y += A_e[k] ; } s *= 0.5 ; } return y ; }
Auch andere Logarithmen lassen sich ohne Mehraufwand berechnen. Enthält die Tabelle die Werte für einen anderen Logarithmus als den zur Basis e, dann berechnet die Funktionen eben diesen Logarithmus (Tabelle A_2 im Anhang):
double Logarithmus_2 ( const double Argument, int N = 53 ) // 1 <= Argument <= 4.768462058 { double x = 1. ; double y = 0. ; double z ; double s = 1. ; int k ; for ( k = 0; k < N; k++ ) { z = x + x*s ; if ( z <= Argument ) { x = z ; y += A_2[k] ; } s *= 0.5 ; } return y ; }
Der erlaubte Bereich für das Argument ist der gleiche (1 < Argument < 4,768...). Im Fall des Logarithmus zur Basis 2 kann man den Exponenten vorher abtrennen (erhält damit den ganzzahligen Anteil des Logarithmus) und wendet auf das Restargument (welches zwischen 1 und 2 liegt) den Bitalgorithmus an. Da das Argument kleiner als 2.384231... ist, braucht die Iterationsschleife von k erst bei 1 anzufangen.
Exponentialfunktion
Um die Exponentialfunktion zu berechnen, dies wird bei dem BKM-Algorithmus auch als E-mode bezeichnet, wird in jedem Schritt getestet, ob
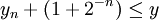 ist. Wenn ja, wird xn + 1 und yn + 1 berechnet. Nach N Schritten ist der Funktionswert mit einem Fehler
ist. Wenn ja, wird xn + 1 und yn + 1 berechnet. Nach N Schritten ist der Funktionswert mit einem Fehler 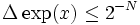 bestimmt.
bestimmt.Beispiel als C++-Programm (Tabelle A_e im Anhang):
double Exponential ( const double Argument, int N = 54 ) // 0 <= Argument <= 1.5620238332 { double x = 1. ; double y = 0. ; double z ; double s = 1. ; int k ; for ( k = 0; k < N; k++ ) { z = y + A_e[k] ; if ( z <= Argument ) { y = z ; x = x + x*s ; } s *= 0.5 ; } return x ; }
Tabellen für die C++-Beispiele
static const double A_e [] = // A_e[k] = ln (1 + 0.5^k) { 0.693147180559945297099404706000, 0.405465108108164392935428259000, 0.223143551314209769962616701000, 0.117783035656383447138088388000, 0.060624621816434840186291518000, 0.030771658666753686222134530000, 0.015504186535965253358272343000, 0.007782140442054949100825041000, 0.003898640415657322636221046000, 0.001951220131261749216850870000, 0.000976085973055458892686544000, 0.000488162079501351186957460000, 0.000244110827527362687853374000, 0.000122062862525677363338881000, 0.000061033293680638525913091000, 0.000030517112473186377476993000, 0.000015258672648362398138404000, 0.000007629365427567572417821000, 0.000003814689989685889381171000, 0.000001907346813825409407938000, 0.000000953673861659188260005000, 0.000000476837044516323000000000, 0.000000238418550679858000000000, 0.000000119209282445354000000000, 0.000000059604642999033900000000, 0.000000029802321943606100000000, 0.000000014901161082825400000000, 0.000000007450580569168250000000, 0.000000003725290291523020000000, 0.000000001862645147496230000000, 0.000000000931322574181798000000, 0.000000000465661287199319000000, 0.000000000232830643626765000000, 0.000000000116415321820159000000, 0.000000000058207660911773300000, 0.000000000029103830456310200000, 0.000000000014551915228261000000, 0.000000000007275957614156960000, 0.000000000003637978807085100000, 0.000000000001818989403544200000, 0.000000000000909494701772515000, 0.000000000000454747350886361000, 0.000000000000227373675443206000, 0.000000000000113686837721610000, 0.000000000000056843418860806400, 0.000000000000028421709430403600, 0.000000000000014210854715201900, 0.000000000000007105427357600980, 0.000000000000003552713678800490, 0.000000000000001776356839400250, 0.000000000000000888178419700125, 0.000000000000000444089209850063, 0.000000000000000222044604925031, 0.000000000000000111022302462516, 0.000000000000000055511151231258, 0.000000000000000027755575615629, 0.000000000000000013877787807815, 0.000000000000000006938893903907, 0.000000000000000003469446951954, 0.000000000000000001734723475977, 0.000000000000000000867361737988, 0.000000000000000000433680868994, 0.000000000000000000216840434497, 0.000000000000000000108420217249, 0.000000000000000000054210108624, 0.000000000000000000027105054312, } ;
static const double A_2 [] = // A_2[k] = log_2 (1 + 0.5^k) { 1.0000000000000000000000000000000000000000000000000000000000000000000000000000, 0.5849625007211561814537389439478165087598144076924810604557526545410982276485, 0.3219280948873623478703194294893901758648313930245806120547563958159347765589, 0.1699250014423123629074778878956330175196288153849621209115053090821964552970, 0.0874628412503394082540660108104043540112672823448206881266090643866965081686, 0.0443941193584534376531019906736094674630459333742491317685543002674288465967, 0.0223678130284545082671320837460849094932677948156179815932199216587899627785, 0.0112272554232541203378805844158839407281095943600297940811823651462712311786, 0.0056245491938781069198591026740666017211096815383520359072957784732489771013, 0.0028150156070540381547362547502839489729507927389771959487826944878598909400, 0.0014081943928083889066101665016890524233311715793462235597709051792834906001, 0.0007042690112466432585379340422201964456668872087249334581924550139514213168, 0.0003521774803010272377989609925281744988670304302127133979341729842842377649, 0.0001760994864425060348637509459678580940163670081839283659942864068257522373, 0.0000880524301221769086378699983597183301490534085738474534831071719854721939, 0.0000440268868273167176441087067175806394819146645511899503059774914593663365, 0.0000220136113603404964890728830697555571275493801909791504158295359319433723, 0.0000110068476674814423006223021573490183469930819844945565597452748333526464, 0.0000055034343306486037230640321058826431606183125807276574241540303833251704, 0.0000027517197895612831123023958331509538486493412831626219340570294203116559, 0.0000013758605508411382010566802834037147561973553922354232704569052932922954, 0.0000006879304394358496786728937442939160483304056131990916985043387874690617, 0.0000003439652607217645360118314743718005315334062644619363447395987584138324, 0.0000001719826406118446361936972479533123619972434705828085978955697643547921, 0.0000000859913228686632156462565208266682841603921494181830811515318381744650, 0.0000000429956620750168703982940244684787907148132725669106053076409624949917, 0.0000000214978311976797556164155504126645192380395989504741781512309853438587, 0.0000000107489156388827085092095702361647949603617203979413516082280717515504, 0.0000000053744578294520620044408178949217773318785601260677517784797554422804, 0.0000000026872289172287079490026152352638891824761667284401180026908031182361, 0.0000000013436144592400232123622589569799954658536700992739887706412976115422, 0.0000000006718072297764289157920422846078078155859484240808550018085324187007, 0.0000000003359036149273187853169587152657145221968468364663464125722491530858, 0.0000000001679518074734354745159899223037458278711244127245990591908996412262, 0.0000000000839759037391617577226571237484864917411614198675604731728132152582, 0.0000000000419879518701918839775296677020135040214077417929807824842667285938, 0.0000000000209939759352486932678195559552767641474249812845414125580747434389, 0.0000000000104969879676625344536740142096218372850561859495065136990936290929, 0.0000000000052484939838408141817781356260462777942148580518406975851213868092, 0.0000000000026242469919227938296243586262369156865545638305682553644113887909, 0.0000000000013121234959619935994960031017850191710121890821178731821983105443, 0.0000000000006560617479811459709189576337295395590603644549624717910616347038, 0.0000000000003280308739906102782522178545328259781415615142931952662153623493, 0.0000000000001640154369953144623242936888032768768777422997704541618141646683, 0.0000000000000820077184976595619616930350508356401599552034612281802599177300, 0.0000000000000410038592488303636807330652208397742314215159774270270147020117, 0.0000000000000205019296244153275153381695384157073687186580546938331088730952, 0.0000000000000102509648122077001764119940017243502120046885379813510430378661, 0.0000000000000051254824061038591928917243090559919209628584150482483994782302, 0.0000000000000025627412030519318726172939815845367496027046030028595094737777, 0.0000000000000012813706015259665053515049475574143952543145124550608158430592, 0.0000000000000006406853007629833949364669629701200556369782295210193569318434, 0.0000000000000003203426503814917330334121037829290364330169106716787999052925, 0.0000000000000001601713251907458754080007074659337446341494733882570243497196, 0.0000000000000000800856625953729399268240176265844257044861248416330071223615, 0.0000000000000000400428312976864705191179247866966320469710511619971334577509, 0.0000000000000000200214156488432353984854413866994246781519154793320684126179, 0.0000000000000000100107078244216177339743404416874899847406043033792202127070, 0.0000000000000000050053539122108088756700751579281894640362199287591340285355, 0.0000000000000000025026769561054044400057638132352058574658089256646014899499, 0.0000000000000000012513384780527022205455634651853807110362316427807660551208, 0.0000000000000000006256692390263511104084521222346348012116229213309001913762, 0.0000000000000000003128346195131755552381436585278035120438976487697544916191, 0.0000000000000000001564173097565877776275512286165232838833090480508502328437, 0.0000000000000000000782086548782938888158954641464170239072244145219054734086, 0.0000000000000000000391043274391469444084776945327473574450334092075712154016, 0.0000000000000000000195521637195734722043713378812583900953755962557525252782, 0.0000000000000000000097760818597867361022187915943503728909029699365320287407, 0.0000000000000000000048880409298933680511176764606054809062553340323879609794, 0.0000000000000000000024440204649466840255609083961603140683286362962192177597, 0.0000000000000000000012220102324733420127809717395445504379645613448652614939, 0.0000000000000000000006110051162366710063906152551383735699323415812152114058, 0.0000000000000000000003055025581183355031953399739107113727036860315024588989, 0.0000000000000000000001527512790591677515976780735407368332862218276873443537, 0.0000000000000000000000763756395295838757988410584167137033767056170417508383, 0.0000000000000000000000381878197647919378994210346199431733717514843471513618, 0.0000000000000000000000190939098823959689497106436628681671067254111334889005, 0.0000000000000000000000095469549411979844748553534196582286585751228071408728, 0.0000000000000000000000047734774705989922374276846068851506055906657137209047, 0.0000000000000000000000023867387352994961187138442777065843718711089344045782, 0.0000000000000000000000011933693676497480593569226324192944532044984865894525, 0.0000000000000000000000005966846838248740296784614396011477934194852481410926, 0.0000000000000000000000002983423419124370148392307506484490384140516252814304, 0.0000000000000000000000001491711709562185074196153830361933046331030629430117, 0.0000000000000000000000000745855854781092537098076934460888486730708440475045, 0.0000000000000000000000000372927927390546268549038472050424734256652501673274, 0.0000000000000000000000000186463963695273134274519237230207489851150821191330, 0.0000000000000000000000000093231981847636567137259618916352525606281553180093, 0.0000000000000000000000000046615990923818283568629809533488457973317312233323, 0.0000000000000000000000000023307995461909141784314904785572277779202790023236, 0.0000000000000000000000000011653997730954570892157452397493151087737428485431, 0.0000000000000000000000000005826998865477285446078726199923328593402722606924, 0.0000000000000000000000000002913499432738642723039363100255852559084863397344, 0.0000000000000000000000000001456749716369321361519681550201473345138307215067, 0.0000000000000000000000000000728374858184660680759840775119123438968122488047, 0.0000000000000000000000000000364187429092330340379920387564158411083803465567, 0.0000000000000000000000000000182093714546165170189960193783228378441837282509, 0.0000000000000000000000000000091046857273082585094980096891901482445902524441, 0.0000000000000000000000000000045523428636541292547490048446022564529197237262, 0.0000000000000000000000000000022761714318270646273745024223029238091160103901, } ;
Einzelnachweise
- ↑ J.C. Bajard, S. Kla und Jean-Michel Muller: A new hardware algorithm for complex elementary functions. IEEE Transactions on Computers 43(8), 1994, S. 955 bis 963.
Literatur
- Jean-Michel Muller: Elementary Functions - Algorithms and Implementation. 2. Auflage. Birkhäuser, 2006, ISBN 0-8176-4372-9.
Weblinks
Wikimedia Foundation.