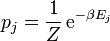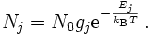Boltzmann-Verteilung

Die Boltzmann-Statistik (auch: Gibbs-Boltzmann-Verteilung, nach Josiah Willard Gibbs und Ludwig Boltzmann) gibt die Wahrscheinlichkeit eines Zustandes eines Systems an, welches im thermodynamischen Gleichgewicht an ein Wärmebad der Temperatur T gekoppelt, also ein Repräsentant eines kanonischen Ensembles, ist.

Wir nehmen dabei an, dass die Zustände durchnummeriert sind mit j = 1,2,...N, mit der jeweils zugehörigen Energie E_j. Die Wahrscheinlichkeit, dass man den Zustand j misst, ist

$p_j=\frac{1}{Z}\, {\rm e}^{-\beta E_j}$

wobei die Normierung Z auch Zustandssumme genannt wird. Man erhält die Boltzmann-Statistik aus der Annahme der a priori gleich wahrscheinlichen Zustände im abgeschlossenen Gesamtsystem, welches das Wärmebad und das betrachtete (Unter-)System, das sich im thermischen Gleichgewicht mit dem Wärmebad befindet, enthält. Die dabei unbestimmt bleibende Konstante β erhält man durch Anschluss an die Thermodynamik: β = 1 / k_BT, mit der Boltzmann-Konstante k_B.

Anstelle von Wahrscheinlichkeiten lässt sich die Boltzmann-Statistik auch durch Teilchenzahlen ausdrücken:

$N_j = N_0 g_j {\rm e}^{-\frac{E_j}{k_{\rm B} T}} \, .$

Hierbei bezeichnet N_j die Zahl der Teilchen, die den Zustand j besetzen, N₀ die Teilchenzahl des 0-ten Zustands und g_j den Entartungsgrad des Zustands j (also die Anzahl von Zuständen gleicher Energie E_j).

Die Boltzmann-Statistik ist anwendbar für alle möglichen klassischen und quantenmechanischen Systeme: magnetische Eigenschaften in Festkörpern, Phononen, Gase usw. Sie definiert u. a. die Empfindlichkeit spektroskopischer Methoden (vgl. NMR).

Für klassische Systeme wie z. B. ideale Gase wird die Darstellung schwieriger, da die Energien der Zustände kontinuierlich dicht liegen und damit aus der Wahrscheinlichkeit eine Wahrscheinlichkeitsdichte wird. Dabei muss das richtige Maß gefunden werden, was Gibbs heuristisch mit 1 / h³ pro Teilchen angegeben hat, was allerdings erst durch die später entstandene Quantentheorie sinnvoll interpretiert werden konnte: das hier eingeführte h wurde das Plancksche Wirkungsquantum.

Der zu den Zuständen gehörige 6N-dimensionale Phasenraum ist durch die Menge aller kontinuierlichen Orte und Impulse aller Gasteilchen gegeben. Das heißt, wenn die Zustandssumme über ein Phasenraumintegral berechnet wird, muss entsprechend die Vielfachheit des Zustandes berücksichtigt werden, was in einem Gas mit N ununterscheidbaren Teilchen einfach 1 / N! ist. Dies nennt man auch die korrigierte Boltzmannabzählung.

Weblinks

• Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart