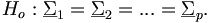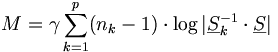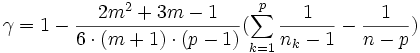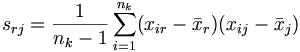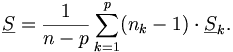Box's M-Test

Der Boxsche M-Test ist ein Verfahren aus der mathematischen Statistik. Er wird in den multivariaten Verfahren angewendet, beispielsweise bei der Diskriminanzanalyse zum Test auf Gleichheit von Streungen in Gruppen.

Seien p viele Zufallsvektoren X_k (k = 1, ... , p) mit jeweils m Komponenten X_j gegeben. Die Vektoren sind alle mit einem Erwartungswertvektor μ_k und einer Kovarianzmatrix Σ_k verteilt.

Die Hypothese soll geprüft werden, dass alle Kovarianzmatrizen gleich sind, also

$H_o: \underline \Sigma_1 = \underline \Sigma_2 = ... = \underline \Sigma_p.$

Die Prüfgröße für den Test ist das so genannte M von Box,

$M= \gamma \sum _{k=1}^p(n_k - 1) \cdot \log|\underline S_k^{-1} \cdot \underline S|$

wobei

$\gamma =1- \frac {2m^2 + 3m-1} {6 \cdot (m + 1) \cdot (p-1)} (\sum _{k=1}^p \frac {1} {n_k -1} - \frac {1} {n-p} )$

als Korrektur dient. Die Kovarianzmatrix S_k wird geschätzt mit den Komponenten

$s_{rj} = \frac {1} {n_k-1} \sum_{i=1}^{n_k} (x_{ir}- \bar x_r) (x_{ij}- \bar x_j)$

und die gepoolte, also mittlere, Kovarianzmatrix durch

$\underline S=\frac {1}{n-p} \sum_{k=1}^p (n_k - 1) \cdot \underline S_k .$

Bei jeweils genügend großem n_k ist die Prüfgröße annähernd χ²-verteilt mit m(m+1)(p-1)/2 Freiheitsgraden. Wenn die S_k sich insgesamt sehr von S unterscheiden, wird der Wert der Prüfgröße hoch. H_o wird also beim Signifikanzniveau α abgelehnt, wenn M größer ist als das 1-α-Quantil der χ²-Verteilung mit m(m+1)(p-1)/2 Freiheitsgraden.