Quantil

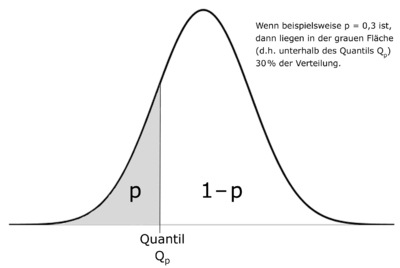
Ein p-Quantil ist ein Lagemaß in der Statistik, wobei p eine reelle Zahl zwischen 0 und 1 ist. Das p-Quantil ist ein Merkmalswert, der die Verteilung einer Variablen bzw. Zufallsvariablen in zwei Abschnitte unterteilt. Links vom p-Quantil liegen $100\cdot p$ Prozent aller Beobachtungswerte bzw. $100\cdot p$ Prozent der Gesamtzahl der Zufallswerte. Rechts davon liegen $100\cdot(1-p)$ Prozent aller Beobachtungswerte bzw. $100\cdot(1-p)$ Prozent der Gesamtzahl der Zufallswerte. p heißt auch der Unterschreitungsanteil.

Spezielle Quantile sind der Median, die Quartile, die Quintile, die Dezile und die Perzentile.

Definition

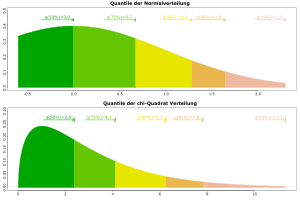Quantile als Umkehrfunktion der Verteilungsfunktion: Zwei Beispiele: Einmal die Standardnormalverteilung und einmal eine Chi-Quadrat-Verteilung mit drei Freiheitsgraden (schiefe Verteilung). Den jeweiligen Wahrscheinlichkeiten werden ihre Quantile zugeordnet; die Fläche unter der abgebildeten Dichte von minus Unendlich bis zum Quantil ist der jeweilige Wert.

Als Quantil der Ordnung p oder p-Quantil (Q_p; veraltet auch „Fraktil“) wird in der Statistik ein Merkmalswert bezeichnet, unterhalb dessen ein vorgegebener Anteil p aller Fälle der Verteilung liegt. Jeder Wert unterhalb von Q_p unterschreitet diesen vorgegebenen Anteil. Deshalb wird p auch als Unterschreitungsanteil bezeichnet. Dabei ist p eine reelle Zahl zwischen 0 (gar kein Fall der Verteilung) und 1 (alle Fälle oder 100 % der Verteilung).

Allgemeiner wird in der Mathematik das p-Quantil wie folgt definiert. Sei X eine Zufallsvariable und F ihre Verteilungsfunktion, so heißt für $p\in(0,1)$ die durch

$F^{-1}(p):=\inf\{x\in\R:F(x)\ge p\}$

definierte Funktion F ^{− 1} Quantilfunktion. F ^{− 1}(p) wird als p-Quantil von F (oder X) bezeichnet.

Beispiel

Das Quantil Q_.3 (oder 0,3-Quantil) ist der Wert des Punktes einer Verteilung, unterhalb dessen sich 30 % aller Fälle der Verteilung befinden.

Ein p-Quantil mit Unterschreitungsanteil

Berechnung empirischer Quantile

Empirische Quantile teilen die Daten einer Messreihe prozentual in zwei Teile, sodass $p \cdot 100%$ der Daten links vom Quantil und $(1 - p) \cdot 100%$ der Daten rechts vom Quantil liegen. Angenommen die Messdaten sind geordnet in Form einer Rangliste gegeben: x₁,x₂,...,x_n. Sei weiter 0 < p < 1. Die Formel für die Berechnung eines p-Quantils ist dann wie folgt:

$\tilde x_p = \begin{cases} \frac{1}{2}(x_{n \cdot p} + x_{n \cdot p + 1}), & \text{wenn }n \cdot p\text{ ganzzahlig,}\\ x_{\lceil n \cdot p \rceil}, & \text{wenn }n \cdot p\text{ nicht ganzzahlig.} \end{cases}$

Dabei ist für eine reelle Zahl x der Wert $\lceil x \rceil$ die kleinste ganze Zahl, die größer oder gleich x ist (siehe auch: Gaußklammer#Aufrundungsfunktion). ^[1][2][3]

• Beispiel 1:

$\begin{align} & x_1,...,x_{10} = (1,1,1,3,4,7,9,11,13,13), ~ p = 0,3 \\ & n \cdot p = 10 \cdot 0,3 = 3 \text{ ist ganzzahlig} \rightarrow \tilde x_{0,3} = \frac{1}{2}(x_{n \cdot p} + x_{n \cdot p + 1}) = \frac{1}{2}(x_3 + x_4) = \frac{1}{2}(1 + 3) = 2 \end{align}$

• Beispiel 2:

$\begin{align} & x_1,...,x_{10} = (1,1,1,3,4,7,9,11,13,13), ~ p = 0,75 \\ & n \cdot p = 10 \cdot 0,75 = 7,5 \text{ ist nicht ganzzahlig} \rightarrow \tilde x_{0,75} = x_{\lceil n \cdot p \rceil} = x_{\lceil 7,5 \rceil} = x_8 = 11 \end{align}$

Besondere Quantile

Für einige bestimmte p haben die p-Quantile zusätzliche Bezeichnungen.

Median

Der Median oder Zentralwert entspricht dem Quantil Q_.5 (0,5-Quantil). Es erfolgt also eine Einteilung der gesamten Verteilung in zwei gleich große Teile. Bei jeder Einteilung in eine ungerade Anzahl von p-Quantilen mit äquidistant-verteilten p (was eine gerade Anzahl gleich großer Teile impliziert) entspricht der Median jeweils dem mittleren Quantil (beispielsweise dem 2. Quartil Q2 oder dem 50. Perzentil P50).

Quartil

Darstellung des Interquartilabstands einer Normalverteilung.

Quartile (lat. „Viertelwerte“) sind die Quantile Q_.25 (0,25-Quantil), Q_.5 (0,5-Quantil=Median) und Q_.75 (0,75-Quantil), die auch als Q1 („unteres Quartil“), Q2 („mittleres Quartil“) und Q3 („oberes Quartil“) bezeichnet werden. Sie sind die in der Statistik mit am häufigsten verwendete Form der Quantile.

Der (Inter-)Quartilabstand oder auch (Inter-)Quartilsabstand (engl. interquartile range) bezeichnet die Differenz zwischen dem oberen und dem unteren Quartil, also Q_.75 − Q_.25 und umfasst daher 50 % der Verteilung. Der Quartilabstand wird als Streuungsmaß verwendet.

Siehe auch: Streuung (Statistik)

Quintil

Durch Quintile (lat. „Fünftelwerte“) wird die Verteilung in 5 gleich große Teile zerlegt. Unterhalb des ersten Quintils, d. h. des Quantils Q_.2, liegen 20 % der Verteilung, unterhalb des zweiten Quintils (Quantil Q_.4) 40 % usw.

Dezil

Durch Dezile (lat. „Zehntelwerte“) wird die Verteilung in 10 gleich große Teile zerlegt. Entsprechend liegen dann z. B. unterhalb des dritten Dezils (Quantil Q_.3) 30 % der Verteilung. Dezile teilen ein der Größe nach geordnetes Datenbündel in 10 gleich große Teile. Das 10-%-Dezil (oder 1. Dezil) gibt an, welcher Wert die unteren 10 % von den oberen 90 % der Datenwerte trennt, das 2. Dezil, welcher Wert die unteren 20 % von den oberen 80 % der Werte trennt, usw. Der Abstand zwischen dem 10-%-Dezil und dem 90-%-Dezil heißt Interdezilbereich.

Perzentil

Durch Perzentile (lat. „Hundertstelwerte“), auch Prozentränge genannt, wird die Verteilung in 100 gleich große Teile zerlegt. Perzentile teilen die Verteilung also in 1-%-Segmente auf. Daher können Perzentile als Quantile betrachtet werden, bei denen $100 \cdot p$ eine ganze Zahl ist. So entspricht das Quantil Q_.97 dem Perzentil P97: unterhalb dieses Punktes liegen 97 % aller Fälle der Verteilung.

a-Fraktil

Für a aus (0,1) wird das (1 − a)-Quantil auch als a-Fraktil bezeichnet. Diese Unterteilung wird z. B. in der als „Paretoprinzip“ bezeichneten Vermutung verwendet.

Beispiele

• Wenn eine Schule 141 Schüler hat, so hat derjenige Schüler den Alters-Prozentrang von 50, der älter ist als die 70 jüngeren Schüler, aber jünger als die 70 älteren Schüler. Ein Prozentrang von 50 oder das 50. Perzentil entspricht dem 0,5-Quantil, also dem Median.
  Für den Prozentrang ist unerheblich, welche Altersunterschiede zwischen den Schülern bestehen; der Prozentrang gibt nur Auskunft über die Position des Einzelnen innerhalb der Gruppe (Stichprobe). Das Alter der Person mit Prozentrang 50 ist deshalb nicht identisch mit dem Durchschnittsalter der betrachteten Gruppe. Deshalb würde sich am Median auch nichts ändern, wenn man die älteren 70 Schüler durch 70 Rentner ersetzen würde.
• In einer Schulklasse sind 13 Aufsätze geschrieben worden, mit der folgenden (sortierten) Notenverteilung:

   Aufsatz A B C D E F G H I J K L M
   Note    1 2 2 2 3 3 3 4 4 4 4 5 6

Die Noten der Aufsätze D („2“), G („3“) und J („4“) entsprechen jeweils Q1, Q2 (d. h. dem Median) und Q3. Der Durchschnitt ist aber ≈ 3.31 (43/13), eine Zahl, die in der Liste gar nicht vorkommt.

• Wird die Körpergröße eines Kindes als Perzentil ausgedrückt, bedeutet dies, dass die Körpergröße in Bezug auf die Körpergrößen der Altersgenossen angegeben wird. Eine Körpergröße auf dem 20. Perzentil bedeutet beispielsweise, dass 20 % der Kinder gleichen Alters und gleichen Geschlechts nicht größer als das betreffende Kind sind (80 % sind größer).

Siehe auch

• Modalwert
• Median
• Parameter (Statistik)
• Boxplot zur grafischen Darstellung
• Value at Risk
• Cornish-Fisher-Methode

Literatur

• Hans-Otto Georgii: Stochastik. 2 Auflage. de Gruyter, Berlin 2004, ISBN 3110182823, S. 225 (Definition Quantil, Quartil, a-Fraktil.).

Einzelnachweise

1. ↑ Berechnung von Median und Quartilen, Medizinische Universität Wien
2. ↑ Udo Bankhofer, Jürgen Vogel: Datenanalyse und Statistik: Eine Einführung für Ökonomen im Bachelor, Gabler Verlag, Wiesbaden 2008, S. 39
3. ↑ Regina Storm: Wahrscheinlichkeitsrechnung, mathematische Statistik und statistische Qualitätskontrolle, Hanser Verlag, München 2007, S. 118