- Break-even-Point
-
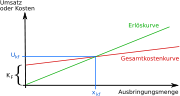
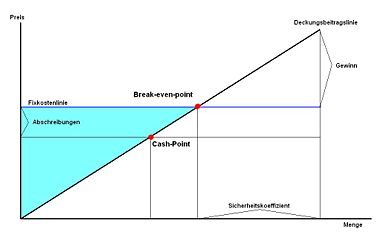
Die Gewinnschwelle oder der Break-even-Point ist in der Wirtschaftswissenschaft der Punkt, an dem Erlös und Kosten einer Produktion (oder eines Produktes) gleich hoch sind und somit weder Verlust noch Gewinn erwirtschaftet wird. Vereinfachend kann man behaupten, dass an der Gewinnschwelle der Deckungsbeitrag aller abgesetzten Produkte identisch mit den Fixkosten ist. Wird die Gewinnschwelle überschritten, macht man Gewinne, wird sie unterschritten, macht man Verluste. Die Gewinnschwelle kann für ein Produkt (Ein-Produkt-Betrachtung) oder mehrere Produkte (Mehr-Produkt-Betrachtung) berechnet werden.
Ausgangspunkt der Gewinnschwellenanalyse sind die Fragestellungen
- Wie viele Produkte müssen produziert und abgesetzt werden, um die Fixkosten zu decken? (Ein-Produkt-Betrachtung)
- Wie viel Umsatz muss durch die betrachteten Produkte erwirtschaftet werden, um die Fixkosten zu decken? (Mehr-Produkt-Betrachtung)
Die Gewinnschwellenanalyse (Break-even-Analyse) ist ein wichtiges Instrument für die Unternehmensplanung. Sie hilft, den Einfluss von Änderungen der Kostenstruktur zu analysieren und die Anforderungen an die Absatzmenge festzustellen.
Inhaltsverzeichnis
Ein-Produkt-Betrachtung
Es sei:
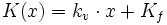 die Kostenfunktion
die Kostenfunktion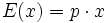 die Erlösfunktion
die Erlösfunktion
K(x) = E(x) -> nach x auflösen. Das ist die Gewinnschwelle.
wobei:
- kv: variable Stückkosten
- Kf: gesamte fixe Kosten
- p: Preis pro Produkteinheit
- x: Produktions-/Absatzmenge des Produkts
Daraus ergibt sich folgender Wert für die Gewinnschwelle xG:
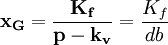
Es müssen also xG Produkte abgesetzt werden, um alle Kosten zu decken. Die Differenz zwischen dem Verkaufserlös (Preis) und den variablen Stückkosten wird auch als Deckungsbeitrag pro Mengeneinheit (db) bezeichnet. Geometrisch entspricht die Gewinnschwelle dem Schnittpunkt der Kostenfunktion mit der Umsatzfunktion.
Mehr-Produkt-Betrachtung
Wenn man mehrere Produkte betrachtet, kann die Gewinnschwelle nicht mehr durch die Menge an abgesetzten Produkten angegeben werden, da die Gewinnschwelle durch mehrere verschiedene Absatzmengen der einzelnen Produktarten erreicht werden kann. Deshalb wird hier der zu erzielende Umsatz verwendet, der durch die Produkte erwirtschaftet werden muss.
Es ergibt sich dann folgende Formel für die Gewinnschwelle:
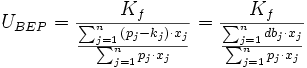
wobei
UBEP: Umsatz, der erzielt werden muss, um die Gewinnschwelle zu erreichen
n: Anzahl der Produktarten
pj: Verkaufspreis von Produkt j
kj: variable Kosten von Produkt j
xj: Produktions-/Absatzmenge von Produkt j
dbj: Deckungsbeitrag von Produkt j
Umgangssprachlich
Umgangssprachlich bezeichnet die Gewinnschwelle auch
- das monetäre Erreichen der Gewinnschwelle eines Unternehmens (d.h. keine Stückzahl, sondern einen Zeitpunkt)
- den Kurs, bei dem ein Wertpapierdepot unter Berücksichtigung der Fixkosten die Gewinnzone erreicht (Gewinnschwellenkurs bzw. Break-even-Kurs)
Prämissen
Die Break-even-Point-Analyse geht von bestimmten Prämissen aus:
- linearer Gesamtkostenverlauf
- Aufteilung der Kosten in variable und fixe Kosten
- Produktionsmenge = Absatzmenge, Lagerhaltung muss additiv berechnet werden
- konstante Verkaufspreise im Laufe der Abrechnungsperiode
- konstantes Produktionsprogramm im Laufe der Abrechnungsperiode
- Gegenüberstellung von positiver und negativer Wirkung
Siehe auch
Wikimedia Foundation.