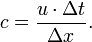CFL-Zahl — Die Courant Friedrichs Lewy Zahl (CFL Zahl oder auch Courant Zahl) wird in der numerischen Strömungssimulation für die Diskretisierung zeitabhängiger partieller Differentialgleichungen verwendet. Sie gibt an, um wie viele Zellen sich eine… … Deutsch Wikipedia
Courant-Friedrichs-Lewy-Bedingung — Die Courant Friedrichs Lewy Zahl (CFL Zahl oder auch Courant Zahl) wird in der numerischen Strömungssimulation für die Diskretisierung zeitabhängiger partieller Differentialgleichungen verwendet. Sie gibt an, um wieviele Zellen sich eine… … Deutsch Wikipedia
Euler-Gleichung — Die Euler Gleichungen oder auch eulersche Gleichungen (nach Leonhard Euler) sind ein mathematisches Modell zur Beschreibung der Strömung von reibungsfreien Fluiden. Es handelt sich um ein partielles Differentialgleichungssystem 1. Ordnung, das… … Deutsch Wikipedia
Eulergleichungen — Die Euler Gleichungen oder auch eulersche Gleichungen (nach Leonhard Euler) sind ein mathematisches Modell zur Beschreibung der Strömung von reibungsfreien Fluiden. Es handelt sich um ein partielles Differentialgleichungssystem 1. Ordnung, das… … Deutsch Wikipedia
Eulersche Bewegungsgleichung — Die Euler Gleichungen oder auch eulersche Gleichungen (nach Leonhard Euler) sind ein mathematisches Modell zur Beschreibung der Strömung von reibungsfreien Fluiden. Es handelt sich um ein partielles Differentialgleichungssystem 1. Ordnung, das… … Deutsch Wikipedia
Euler-Gleichungen — Die Euler Gleichungen oder auch eulersche Gleichungen (nach Leonhard Euler) sind ein mathematisches Modell zur Beschreibung der Strömung von reibungsfreien Fluiden. Es handelt sich um ein partielles Differentialgleichungssystem 1. Ordnung, das… … Deutsch Wikipedia
Gleichungen von Navier-Stokes — Die Navier Stokes Gleichungen [navˈjeː stəʊks] (nach Claude Louis Marie Henri Navier und George Gabriel Stokes) sind die Grundgleichungen der Strömungsmechanik. Sie beschreiben die Strömung in newtonschen Flüssigkeiten und Gasen. Die Navier… … Deutsch Wikipedia
Navier-Stokes-Gleichung — Die Navier Stokes Gleichungen [navˈjeː stəʊks] (nach Claude Louis Marie Henri Navier und George Gabriel Stokes) sind die Grundgleichungen der Strömungsmechanik. Sie beschreiben die Strömung in newtonschen Flüssigkeiten und Gasen. Die Navier… … Deutsch Wikipedia
Navier Stokes Gleichungen — Die Navier Stokes Gleichungen [navˈjeː stəʊks] (nach Claude Louis Marie Henri Navier und George Gabriel Stokes) sind die Grundgleichungen der Strömungsmechanik. Sie beschreiben die Strömung in newtonschen Flüssigkeiten und Gasen. Die Navier… … Deutsch Wikipedia
Navier-Stokes-Gleichungen — Die Dispersion und Refraktion von Meereswellen kann mittels der Navier Stokes Gleichung simuliert und berechnet werden.[1] Die Navier Stokes Gleichungen [navˈjeː stəʊks] (nach Claude Louis Marie Henri Navier und … Deutsch Wikipedia