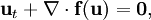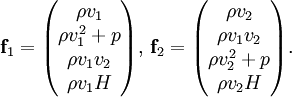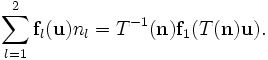Eulersche Bewegungsgleichung

Die Euler-Gleichungen oder auch eulersche Gleichungen (nach Leonhard Euler) sind ein mathematisches Modell zur Beschreibung der Strömung von reibungsfreien Fluiden. Es handelt sich um ein partielles Differentialgleichungssystem 1. Ordnung, das sich als Sonderfall der Navier-Stokes-Gleichungen ergibt, falls Reibung und Wärmeleitung vernachlässigt werden. Der wesentliche Teil ist hierbei der Impulssatz, der unter Vernachlässigung äußerer Kräfte in differentieller Form lautet:

$\frac{\partial \mathbf{v}}{\partial t} + \left( \mathbf{v} \cdot \nabla \right) \mathbf{v} + \frac{1}{\rho} \nabla p = \mathbf{0}$,

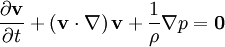wobei 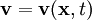$\mathbf{v}=\mathbf{v}(\mathbf{x}, t)$ der Geschwindigkeitsvektor, ρ die Dichte, 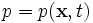$p=p(\mathbf{x},t)$ der Druck, 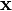$\mathbf{x}$ der Ortsvektor, t die Zeit und $\nabla$ der Nabla-Operator ist.

Die linke Seite der Gleichung beschreibt die substanzielle Beschleunigung, bestehend aus der lokalen und der konvektiven Beschleunigung, die sich aus der Einwirkung etwaiger äußerer Kräfte und der Oberflächenkraft (Druckkraft) ergibt.

Eine ebenfalls übliche Formulierung der Euler-Gleichungen umfasst zusätzlich die skalaren Gleichungen für Massenerhaltung (Kontinuitätsgleichung) und Energieerhaltung. Diese fünf gekoppelten Differentialgleichungen, zusammengenommen mit einer Zustandsgleichung ergeben ein geschlossenes Gleichungssystem, um die fünf unbekannten Größen der Geschwindigkeit 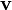$\mathbf{v}$, des Druckes p und der Dichte ρ zu berechnen. Dieses System lautet im zweidimensionalen Fall dann:

$\mathbf{u}_t + \nabla \cdot \mathbf{f}(\mathbf{u}) = \mathbf{0},$

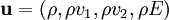wobei $\mathbf{u} = (\rho, \rho v_1, \rho v_2, \rho E)$ der Vektor der Erhaltungsvariablen ist und die Flüsse $\mathbf{f}$ mit der Enthalpie H durch folgende Ausdrücke gegeben sind:

$\mathbf{f}_1 = \begin{pmatrix}\rho v_1 \\ \rho v_1^2 +p \\ \rho v_1 v_2 \\ \rho v_1 H\end{pmatrix}, \, \mathbf{f}_2 = \begin{pmatrix}\rho v_2 \\ \rho v_1v_2 \\ \rho v_2^2 +p \\ \rho v_2 H\end{pmatrix}.$

An festen Wänden wird dabei als Bedingung gesetzt, dass die Geschwindigkeit in Normalenrichtung null ist. An die Tangentialkomponente der Geschwindigkeit kann dann keine zusätzliche Bedingung gesetzt werden, im Gegensatz zu den Navier-Stokes-Gleichungen, bei denen die No-Slip-Bedingung und die Terme zweiter Ordnung eine Grenzschicht erzeugen. Dieses macht gemeinsam mit dem Fehlen von Turbulenz den wesentlichen Unterschied zu den Navier-Stokes-Gleichungen aus.

Herleitung

Die Eulergleichungen können auf verschiedene Weise hergeleitet werden: Ein verbreiteter Ansatz wendet das Transporttheorem von Reynolds auf das zweite newtonsche Axiom an. Das Transporttheorem beschreibt die zeitliche Änderung einer physikalischen Größe in einem bewegten Kontrollvolumen.

Ein weiterer Ansatz geht von der Boltzmann-Gleichung aus: Der Kollisionsoperator wird dort mit drei möglichen Termen multipliziert, den sog. Kollisionsinvarianten. Nach Integration über die Teilchengeschwindigkeit entstehen Kontinuitätsgleichung, Impulsgleichung und Energiebilanz. Schließlich wird eine Skalierung für große Zeit- und Raumabmessungen durchgeführt (Hydrodynamische Limites), und das Ergebnis sind die erweiterten Eulergleichungen.

Mathematische Eigenschaften

Die Eulergleichungen gehören zur Kategorie der nichtlinearen hyperbolischen Erhaltungsgleichungen. Damit treten in der Regel nach endlicher Zeit auch bei glatten Anfangsdaten Unstetigkeiten auf, etwa Schocks (Verdichtungsstöße). Unter starken Voraussetzungen existieren im relevanten Fall ρ,p > 0 globale glatte Lösungen, etwa dann, wenn die Lösung sich in einer Art Verdünnungswelle fortbewegt. Im stationären Fall ist die Gleichung je nach Mach-Zahl elliptisch oder hyperbolisch. Bei einer transsonischen Strömung treten dann sowohl Unterschall als auch Überschallgebiete auf, und die Gleichung hat gemischten Charakter.

Die Eigenwerte der Gleichungen sind die Geschwindigkeit in Normalenrichtung v_n (mit Vielfachheit der Dimension) und diese plus minus die Schallgeschwindigkeit, 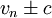$v_n \pm c$. Damit sind die Euler-Gleichungen im eindimensionalen sogar strikt hyperbolisch, so dass es dort brauchbare Existenz- und Eindeutigkeitsresultate gibt. Im mehrdimensionalen sind sie nicht mehr strikt hyperbolisch aufgrund des mehrfachen Eigenwerts und die mathematische Lösung ist extrem schwierig. Hierbei dreht es sich vor allem um das Bestimmen physikalisch sinnvoller schwacher Lösungen, also solcher, die sich als Lösungen der Navier-Stokes-Gleichungen mit verschwindender Viskosität interpretieren lassen.

Darüber hinaus sind die Euler-Gleichungen rotationsinvariant, es gilt also für beliebige Einheitsvektoren $\mathbf{n}$ und für Rotationen der Geschwindigkeiten in Richtung dieser Normalenvektoren:

$\sum_{l=1}^2\mathbf{f}_l(\mathbf{u})n_l = T^{-1}(\mathbf{n}) \mathbf{f}_1(T(\mathbf{n})\mathbf{u}).$

Darüber hinaus sind die Flussfunktionen homogen, es gilt also $\mathbf{f}_l(\mathbf{u}) = \frac{\partial \mathbf{f}_l(\mathbf{u})}{\partial \mathbf{u}}\mathbf{u}$.

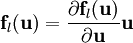Numerische Lösung

Da die Euler-Gleichungen Erhaltungsgleichungen darstellen, werden sie in der Regel mit Hilfe von Finite-Volumen-Verfahren gelöst. Umgekehrt waren die Bemühungen aus dem Bereich der Aerodynamik seit den 1950ern, die Euler-Gleichungen numerisch zu simulieren, treibende Kräfte bei der Entwicklung von Finite-Volumen-Verfahren. Da im Gegensatz zu den Navier-Stokes-Gleichungen keine Grenzschicht berücksichtigt werden muss, kann dies auf vergleichsweise groben Rechengittern passieren. Die zentrale Schwierigkeit stellt die Behandlung des Euler-Flusses dar, der üblicherweise mit Hilfe von approximativen Riemann-Lösern behandelt wird. Diese liefern eine Näherung an die Lösung von Riemann-Problemen entlang von Zellkanten. Das Riemann-Problem der Euler-Gleichungen ist sogar exakt lösbar, allerdings ist die Berechnung dieser Lösung extrem aufwändig. Seit den 1980ern wurden deswegen zahlreiche approximative Löser entwickelt, angefangen mit dem Roe-Löser bis hin zur AUSM-Familie in den 1990ern.

Bei der Zeitintegration ist die CFL-Bedingung zu beachten. Gerade im Bereich von Machzahlen Nahe null oder eins werden die Gleichungen aufgrund der unterschiedlich Eigenwertskalen sehr steif, was den Einsatz impliziter Zeitintegrationsverfahren notwendig macht: die CFL-Bedingung orientiert sich am größten Eigenwert (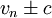$v_n \pm c$), während die für die Simulation relevanten Teile der Strömung sich mit v_n bewegen. Ein explizites Verfahren bräuchte damit in den meisten Fällen inakzeptabel viele Zeitschritte.

Die Lösung dabei auftretender nichtlinearer Gleichungssysteme erfolgt dann entweder mit Hilfe von vorkonditionierten Newton-Krylow-Verfahren oder mit speziellen nichtlinearen Mehrgitter-Verfahren.

Abgeleitete Beziehungen

Aus den erweiterten Eulergleichungen kann eine Reihe gasdynamischer Grundgleichungen abgeleitet werden:

• die Bernoulligleichung,
• die akustische Wellengleichung,
• die inkompressiblen Eulergleichungen.

Diese Gleichungen erhält man insbesondere durch geeignete Skalierung der Eulergleichungen.

Literatur

• E. Godlewski und P.-A. Raviart: Hyperbolic Systems of Conservation Laws, 1991, Ellipses, Paris