CUSUM

In der statistischen Prozess- und Qualitätskontrolle ist die kumulative Summe oder CUSUM (von (engl. “cumulative sum”) eine sequentielle Analysemethode zur Entdeckung von Änderungen in einer sequentiellen Datenreihe oder Zeitreihe (z.B. Kurswechsel bzw. Wendepunkte).^[1].

E. S. Page definierte 1954 eine Qualitätszahl θ, einen Parameter einer Wahrscheinlichkeitsverteilung; z.B. den Erwartungswert. Er entwickelte CUMSUM als Methode, um generelle Änderungen des Parameters aus zufälligem Rauschen heraus zu filtern und schlug ein Grenzkriterium vor ab dem in den Prozess eingegriffen werden sollte. Einige Jahre später stellte George Alfred Barnard das V-Mask Diagramm vor zur visuellen Entdeckung von Änderungen von θ.^[2]

Vorgehensweise

CUSUM betracht die kumulative Summen von Datenwerten x_n und vorgebenen Werten ω_n:

S₀ = 0

S_n = max(0,S_{n − 1} + x_n − ω_n)

Es ist wichtig anzumerken, dass CUSUM nicht die bloße kumulative Summe der Datenwerte ist, sondern die kumulative Summe der Differenzen zwischen den Datenwerten x_n und ω_n. Überschreitet der Wert von S_{n + 1} einen vorgebenen Grenzwert, dann hat man eine Änderung gefunden. CUMSUM erkennt also nicht nur scharfe Datenwertänderungen, sondern auch schrittweise und kontinuierliche über den Betrachtungzeitraum. Meist handelt es sich bei ω um eine Likelihood-Funktion, obwohl dies in Pages Artikel nicht so spezifiziert wird.

Beispiele

Beispiel 1

In dem Beispiel wird vorgegeben ω_n = 5 und betrachtet werden sowohl positive als auch negative kumulierte Abweichungen:

$S_0=S_0^+=S_0^-=0$

$S_{n}^+=\max(0, S_{n-1}^++x_n-\omega_n)$

$S_{n}^-=\max(0, S_{n-1}^-+\omega_n-x_n)$

S_n = S_{n − 1} + ω_n − x_n

Grafische Darstellung der CUSUM Berechnung.

n	Datenwert xn	xn − ωn	$S_n^+$	$S_n^-$	CUSUM Sn
0			0	0	0
1	2	-3	0	3	-3
2	4	-1	0	4	-4
3	7	+2	2	2	-2
4	3	-2	0	4	-4
5	9	+4	4	0	0

S_n kann auch aufgefasst werden:

1. Alle Datenpunkte werden mittelwertbereinigt (x_n − ω_n) und
2. zu jedem dadurch neu entstandenen Wert werden alle vorhergehenden mittelwertbereinigten Differenzen aufaddiert.

Der Mittelwert ist dabei die Likelihoodschätzung für den Erwartungswert normalverteilter Datenwerte.

Beispiel 2

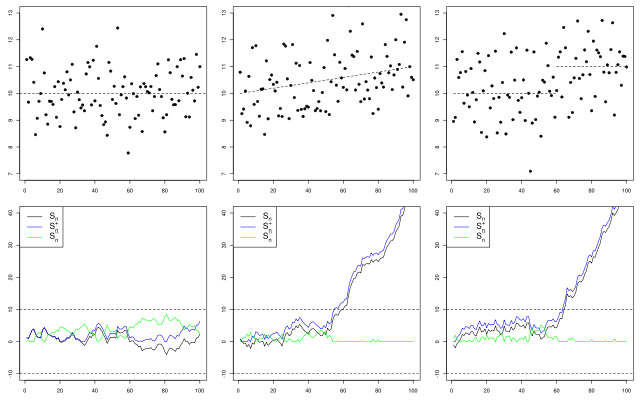
Die folgenden Grafiken zeigen den Verlauf von $S_n\,$, $S_n^+$ und $S_n^-$ in verschiedenen Situationen:

• links: der Mittelwert des Prozesses ändert sich nicht
• mitte: der Mittelwert des Prozesses wird langsam größer (im Verhältnis zur Streuung)
• rechts: der Mittelwert springt abrupt nach oben nach 60 Zeiteinheiten

In den Daten (oben) sind diese Änderungen kaum zu erkennen, jedoch nicht im Verlauf der $S_n\,$, $S_n^+$ und $S_n^-$ Kurven (unten).

Literatur

• Michèle Basseville, Igor V. Nikiforov: Detection of Abrupt Changes: Theory and Application. Prentice-Hall, Englewood Cliffs, N.J. April 1993, ISBN 0-13-126780-9 (http://www.irisa.fr/sisthem/kniga/).
• Douglas M. Hawkins, David H. Olwell: Cumulative sum charts and charting for quality improvement Springer Verlag, 1998, ISBN 0-387-98365-1.

Weblinks

• http://www.medialabinc.net/keyword-details.asp?keyword=CUSUM&courseid=1026
• http://creativecommons.org/licenses/by-sa/3.0/deed.de

Einzelnachweise

1. ↑ E. S. Page: Continuous Inspection Scheme. In: Biometrika. 41, Nr. 1/2, Juni 1954, S. 100–115 (http://links.jstor.org/sici?sici=0006-3444%28195406%2941%3A1%2F2%3C100%3ACIS%3E2.0.CO%3B2-H).
2. ↑ G.A. Barnard: Control charts and stochastic processes. In: Journal of the Royal Statistical Society B (Methodological). 21, Nr. 2, 1959, S. 239–271 (http://links.jstor.org/sici?sici=0035-9246(1959)21%3A2%3C239%3ACCASP%3E2.0.CO%3B2-6).