- Deformationsgradient
-
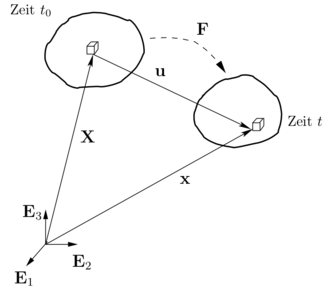
Der Deformationsgradient
 stellt eine tensorielle Abbildung zweier Konfigurationen dar und ist die in der Kontinuumsmechanik grundlegende Größe zur Beschreibung von Verformungen in Körpern aufgrund von Belastungen.
stellt eine tensorielle Abbildung zweier Konfigurationen dar und ist die in der Kontinuumsmechanik grundlegende Größe zur Beschreibung von Verformungen in Körpern aufgrund von Belastungen.Oft wird mit dem Deformationsgradienten die Abbildung eines materiellen Punktes
 (bzw. eines (infinitesimal kleinen) Linienelements
(bzw. eines (infinitesimal kleinen) Linienelements  an
an  ) zum Zeitpunkt
) zum Zeitpunkt  aus der Ausgangs- oder Referenzkonfiguration im Euklidischen Punktraum
aus der Ausgangs- oder Referenzkonfiguration im Euklidischen Punktraum  in die aktuelle oder Momentankonfiguration zu einem späteren Zeitpunkt
in die aktuelle oder Momentankonfiguration zu einem späteren Zeitpunkt  dargestellt. Der Differenz- oder Verschiebungsvektor zwischen
dargestellt. Der Differenz- oder Verschiebungsvektor zwischen  und
und  wird mit
wird mit  gekennzeichnet.
gekennzeichnet.Ganz allgemein kann man sich eine solche Abbildung aber auch zwischen beliebig anderen zu definierenden Konfigurationen vorstellen. Beispiele hierfür finden sich in der Beschreibung der Plastizitätstheorie. Die zeitliche Abfolge und damit fortlaufende Abbildung mit sich möglicherweise auch ändernden Deformationsgradienten wird als Bewegung bezeichnet.
Polare Zerlegung
Der Deformationsgradient
 lässt sich eindeutig "polar" zerlegen. Durch Anwendung der Polarzerlegung erhält man alternativ die Darstellungen
lässt sich eindeutig "polar" zerlegen. Durch Anwendung der Polarzerlegung erhält man alternativ die Darstellungen .
.Dabei wird mit
 eine "eigentlich orthogonale Drehmatrix" bzw. -tensor beschrieben. Mit
eine "eigentlich orthogonale Drehmatrix" bzw. -tensor beschrieben. Mit  wird der (symmetrische) Rechts-Strecktensor bzgl. der Ausgangskonfiguration und analog dazu mit
wird der (symmetrische) Rechts-Strecktensor bzgl. der Ausgangskonfiguration und analog dazu mit  der (symmetrische) Links-Strecktensor bzgl. der Momentankonfiguration beschrieben. (Eselsbrücke:
der (symmetrische) Links-Strecktensor bzgl. der Momentankonfiguration beschrieben. (Eselsbrücke:  steht rechts von
steht rechts von  und
und  links davon in der polaren Darstellung.)
links davon in der polaren Darstellung.)Volumenverhältnis
Die Determinante von
 gibt das Volumenverhältnis
gibt das Volumenverhältnis  des betrachteten materiellen Punktes bei der Deformation an.
des betrachteten materiellen Punktes bei der Deformation an.Damit ergibt sich u.a., dass
 nicht negativ sein/werden kann, sonst wäre die Deformation physikalisch nicht möglich (Inversion des materiellen Punktes).
nicht negativ sein/werden kann, sonst wäre die Deformation physikalisch nicht möglich (Inversion des materiellen Punktes).Bleibt bei einer Deformation das Volumen erhalten, also
 spricht man von Inkompressibilität. Bei Gummi- oder Elastomer-Werkstoffen ist dies eine übliche Annahme in der kontinuumsmechanischen Beschreibung und durch das Verhalten dieser Werkstoffklasse sehr gut gerechtfertigt.
spricht man von Inkompressibilität. Bei Gummi- oder Elastomer-Werkstoffen ist dies eine übliche Annahme in der kontinuumsmechanischen Beschreibung und durch das Verhalten dieser Werkstoffklasse sehr gut gerechtfertigt.Literatur
- J. Altenbach, H.Altenbach: Einführung in die Kontinuumsmechanik. Teubner, Stuttgart 1994, ISBN 3-519-03096-9, S. 38.
Wikimedia Foundation.