- Doubly-connected edge list
-
Die Doubly-connected edge list (DCEL, doppelt verkettete Kantenliste) ist eine Datenstruktur, die einen zusammenhängenden planaren Graphen repräsentiert, der in die Ebene eingebettet ist. Die Datenstruktur wird in der algorithmischen Geometrie verwendet.
Inhaltsverzeichnis
Definition
Sei G = (V,E) ein planarer Graph, V = {v1,v2,...,vn} die Menge der Knoten, E = {e1,e2,...,em} die Menge der Kanten.
Die DCEL speichert für jede Kante ei des Graphens einen Eintrag mit den Daten (V1,V2,F1,F2,P1,P2):
- V1: Startknoten der Kante ei
- V2: Endknoten der Kante ei
- F1: Name der Fläche auf der linken Seite der Kante
- F2: Name der Fläche auf der rechten Seite der Kante
- P1: Zeiger auf die erste Kante mit Knoten V1, auf die man trifft, wenn man die Kante ei gegen den Uhrzeigersinn um V1 dreht
- P2: Analog zu P1, diesmal mit Knoten V2
Beispiel
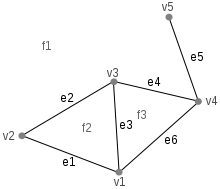
Für den Graphen in der Abbildung werden folgende Einträge gespeichert:
V1 V2 F1 F2 P1 P2 e1 v1 v2 f1 f2 e6 e2 e2 v2 v3 f1 f2 e1 e3 e3 v3 v1 f3 f2 e4 e1 e4 v3 v4 f1 f3 e2 e6 e5 v4 v5 f1 f1 e4 e5 e6 v4 v1 f1 f3 e5 e3 Anwendungen und Sonstiges
Mit Hilfe der Verweise auf die Nachfolgekanten können effizient alle Kanten mit vorgegebenen Endpunkt bestimmt werden, ebenso alle Kanten auf dem Rand einer gegebenen Fläche.
Als Doubly-connected edge list wird ebenfalls die etwas anders aufgebaute Half-Edge-Datenstruktur bezeichnet. DCEL ist eine Variante der winged-edge-Datenstruktur.
Fügt man zusätzlich die Kanten ein, die man erhält, wenn man ei im Uhrzeigersinn um V1 und V2 dreht, erhält man die quad edge data structure (QEDS). Mit ihr lassen sich Ränder von Flächen und von einem Knoten ausgehende Kanten in beide Richtungen durchlaufen. Ein weiterer Vorteil ist, dass man die QEDS des dualen Graphen erhält, wenn jede Kante durch ihre jeweilige duale Kante ersetzt wird.[1]
Literatur
- Franco P. Preparata, Michael Ian Shamos: Computational geometry: an introduction. New York : Springer-Verlag, c1985., ISBN 0387961313, S. 15
- Dinesh P. Mehta, Sartaj Sahni: Handbook of data structures and applications CRC Press, 2004, ISBN 1584884355, S. 17-7
- Rolf Klein: Algorithmische Geometrie: Grundlagen, Methoden, Anwendungen. 2. Auflage. Springer, Berlin, Berlin [u.a.] 2005, ISBN 978-3-5402-0956-0., S. 19
Einzelnachweise
- ↑ Rolf Klein: Algorithmische Geometrie, 2005, S. 19–20.
Wikimedia Foundation.