Dualer Graph

In vielen Bereichen der Mathematik gibt es die folgende Situation: zu jedem Objekt X der jeweils betrachteten Klasse gibt es ein duales Objekt Y = X', dessen duales Objekt Y' = (X')' wiederum X ist oder zumindest X sehr nahe kommt. Häufig gibt es auch noch eine Verbindung zwischen X und Y, die die Beziehung zwischen ihnen näher beschreibt.

Dualität in der Geometrie

Dualität von Polytopen

Zwei Polytope (also Polygone, Polyeder usw.) P und Q heißen kombinatorisch dual, wenn ihre Seitenverbände (die Inklusion ihrer Seiten, also Ecken, Kanten, Flächen usw.) anti-isomorph sind. Dazu ein Beispiel: Wählt man die Mittelpunkte der Seitenflächen eines dreidimensionalen konvexen Polyeders P als Ecken, und verbindet man zwei "neue" Ecken, wenn die beiden entsprechende Seitenflächen von P eine gemeinsame Kante haben, so erhält man ein duales Polyeder Q. Die Eckenzahl von Q ist gleich der Flächenzahl von P und umgekehrt, die Kantenanzahlen sind gleich.

Dies sagt aber nichts darüber aus, ob die Polytope P und Q invariant unter den gleichen Symmetrieabbildungen sind. Ein Quadrat und ein beliebiges Viereck sind beispielsweise kombinatorisch dual, da an jeder Ecke zwei Kanten zusammentreffen und jede Kante zwei Ecken hat. In der Regel gehören zu den Symmetrieabbildungen des Vierecks keine Spiegelungen, für das Quadrat hingegen schon.

Zu jedem Polytop P gibt es ein spezielles kombinatorisch duales Polytop, die so genannte Polare . Hierzu fasst man das Polytop P als abgeschlossene Teilmenge eines euklidischen Vektorraums auf. Die Polare besteht dann aus allen Punkten y, die für alle x von P die Ungleichung 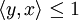$\langle y,x\rangle \le 1$ erfüllen. Unter der Voraussetzung, dass der geometrische Schwerpunkt von P auf der Null liegt, haben P und seine Polare dieselbe Symmetriegruppe. Das doppelt-duale Polyeder ist ähnlich zu P und gleich diesem, wenn der Nullpunkt in seinem Inneren enthalten ist.

Für Beispiele siehe platonischer Körper, archimedischer Körper

Dualitätsprinzip der projektiven Geometrie

In der ebenen projektiven Geometrie gilt folgendes Dualitätsprinzip: Vertauscht man in einer wahren Aussage über Punkte und Geraden einer projektiven Ebene die Begriffe "Punkt" und "Gerade" und ersetzt man jeweils den Begriff "Verbindungsgerade zweier Punkte" durch den Begriff "Schnittpunkt zweier Geraden" und umgekehrt, so erhält man wieder eine wahre Aussage.

Beispiele für Paare dualer Sätze sind der Satz von Desargues und dessen Umkehrung oder der Satz von Pascal und der Satz von Brianchon.

Geometrisch dualer Graph

Eine ähnliche Definition kennt auch die Graphentheorie für planare Graphen. Ein zum Graphen G = (V,E) geometrisch dualer Graph G' = (V',E') entsteht, indem in jeder Fläche des Graphen G neue Knoten v' hinzugefügt werden und für jede Kante 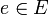$e\in E$ eine neue Kante e' erstellt wird, die die v' der beiden angrenzenden Flächen verbindet.

Ist der Graph G nicht nur planar, sondern auch zusammenhängend, so gilt auch hier, dass die Anzahl der Knoten in G' der Anzahl der Flächen in G entspricht, die Anzahl der Flächen in G' derjenigen der Knoten in G und die Anzahl der Kanten bleibt konstant. Im zusammenhängenden Fall gibt es damit bijektive Abbildungen zwischen den Kantenmengen der beiden Graphen und jeweils den Mengen der Knoten und Flächen. Außerdem gilt, dass G'' = G.

Lineare Algebra: Dualraum eines Vektorraumes

Ist V ein Vektorraum über einem Körper K, so ist der duale Vektorraum oder Dualraum V ^* der Vektorraum, dessen Elemente die linearen Abbildungen 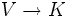$V\to K$ sind. Ist V endlichdimensional, so hat V ^* dieselbe Dimension wie V, und V ^{* *} ist kanonisch isomorph zu V.

Siehe Dualraum

Funktionalanalysis: Dualraum eines Banachraumes

Im Fall eines Banachraumes X besteht der Dualraum X ^* aus den stetigen linearen Funktionalen. Im Allgemeinen ist der Bidualraum X ^{* *} nicht wieder X selbst. Diejenigen Räume, für die X = X ^{* *} gilt, heißen reflexiv; Beispiele sind die Räume L^p für 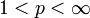$1<p<\infty$ sowie alle Hilberträume.

• Siehe auch: Dualraum

Mengenlehre: Komplementbildung

Eine Dualität, die nicht mit diesem Wort bezeichnet wird, ist die Bildung des Komplementes einer Menge: Ist eine Grundmenge G gegeben, so ist das Komplement einer Teilmenge 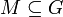$M\subseteq G$ die Menge 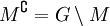$M^\complement=G\setminus M$ der Elemente von G, die nicht in M liegen. Das Komplement des Komplementes ist wieder M selbst. Die Komplementbildung setzt Vereinigungsmenge und Schnittmenge zueinander in Beziehung: 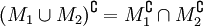$(M_1\cup M_2)^\complement= M_1^\complement\cap M_2^\complement$ (siehe de Morgansche Regeln).

Eine Verallgemeinerung dieses Beispiels stellt die Negation in einer beliebigen booleschen Algebra dar.

Nach dem Dualitätsprinzip für Verbände erhält man aus einer beliebigen wahren Aussage über Teilmengen einer Grundmenge G wieder eine wahre Aussage, wenn man die Symbole 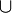$\cup$ (Vereinigungsmenge) und 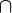$\cap$ (Schnittmenge) sowie die Symbole 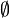$\emptyset$ (leere Menge) und G (Grundmenge) vertauscht.

• Siehe auch: Komplement (Mengenlehre), boolesche Algebra

Siehe auch

• Dualität in der Linearen Optimierung