Abgeschlossen

In der Mathematik tritt der Begriff Abgeschlossenheit in mehreren Bedeutungen auf, die alle in etwa besagen, dass das betreffende Objekt mit den jeweils betrachteten Mitteln nicht erweitert werden kann. Eine Abstraktion dieser Erweiterungsprozesse ist der Begriff des Hüllenoperators.

Abgeschlossene Menge

Ist M eine Teilmenge eines topologischen Raums X, dann heißt M abgeschlossen, falls ihr Komplement 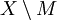$X\setminus M$ eine offene Menge in X ist.

Erfüllt X das erste Abzählbarkeitsaxiom (dies gilt beispielsweise dann, wenn X ein metrischer Raum ist), so ist M genau dann abgeschlossen, wenn M alle Grenzwerte der konvergenten Folgen in X enthält, deren Glieder in M liegen.

Ist X ein beliebiger topologischer Raum, so ist 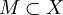$M \subset X$ genau dann abgeschlossen, wenn in M die Grenzwerte aller in X konvergenten Netze liegen, deren Glieder aus M sind.

Abgeschlossen bezüglich einer Verknüpfung

Ist f eine n-stellige innere Verknüpfung auf einer Menge A, dann heißt das: f ist eine Funktion 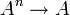$A^n \to A$. Gilt nun 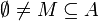$\emptyset \neq M \subseteq A$, dann heißt M abgeschlossen bezüglich f, wenn 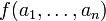$f(a_1,\ldots,a_n)$ in M liegt für alle 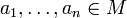$a_1,\ldots,a_n \in M$, wenn also f eingeschränkt auf den Definitionsbereich Mⁿ auch eine n-stellige innere Verknüpfung auf M ist.

Hat man Strukturen mit mehreren Verknüpfungen, dann hat man auch einen Begriff der Abgeschlossenheit bezüglich all dieser Verknüpfungen.

Beispiele:

• Eine Untergruppe ist eine nichtleere Teilmenge einer Gruppe (G, + ), die abgeschlossen bezüglich der Verknüpfung + und der Inversenbildung ist.
• Ein Untervektorraum ist eine nichtleere Teilmenge eines Vektorraums V, die abgeschlossen ist bezüglich der Vektoraddition und der skalaren Multiplikation.
• Allgemein ist eine algebraische Unterstruktur eine (nichtleere) Teilmenge einer algebraischen Struktur, die abgeschlossen ist bezüglich sämtlichen Verknüpfungen dieser Struktur.

Die Wichtigkeit der Abgeschlossenheit bezüglich einer Verknüpfung lässt sich am besten verstehen, wenn man Beispiele betrachtet, in denen sie verletzt ist.

• So ist 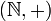$(\mathbb N,+)$ als Unterstruktur der Gruppe 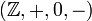$(\mathbb Z,+,0,-)$ nicht abgeschlossen, also keine Untergruppe. Diese Teilmenge ist zwar bezüglich der Addition abgeschlossen, nicht aber bezüglich der Inversenbildung: mit 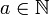$a \in \mathbb N$ gehört − a nicht 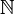$\mathbb N$ an.
• Der Durchschnitt zweier Untervektorräume eines Vektorraums ist stets selbst ein Untervektorraum, jedoch ist die Vereinigung zweier Untervektorräume nicht notwendig ein Untervektorraum. Die Vereinigung ist zwar abgeschlossen bzgl. der skalaren Multiplikation, aber nicht unbedingt bzgl. der Vektoraddition.

Analog dazu ist M auch abgeschlossen gegenüber einer $\infty$-stelligen inneren Verknüpfung f auf A, wenn deren Bild in M liegt.

Beispiel:

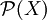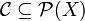• Ist $\mathcal P(X)$ die Potenzmenge einer unendlichen Menge X und $\mathcal C$ die Menge aller abgeschlossenen Mengen (siehe oben) bezüglich einer T₁-Topologie auf X ($\mathcal C \subseteq \mathcal P(X)$ enthält also alle – unendlich viele – einelementigen Teilmengen von X), dann ist $\mathcal C$ eine abgeschlossene Menge bezüglich dem mengentheoretischen Durchschnitt $\bigcap$ auf $\mathcal P(X)$.

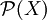Die Eigenschaft, dass eine Verknüpfung f auf einer Menge A stets eindeutig bestimmte Werte in A liefert, bezeichnet man auch als Wohldefiniertheit dieser Verknüpfung.

Deduktive Abgeschlossenheit

In der klassischen Logik bezeichnet man eine Menge F logischer Formeln als deduktiv abgeschlossen, wenn die Menge aller Formeln, die aus einer der Formeln von F logisch folgen, gerade die Menge F ergeben, d. h. Cn(F) = F wobei Cn die so genannte Inferenzoperation ist, d. h. diejenige Operation, die eine Formelmenge F auf die Menge von Formeln abbildet, die logisch aus F folgt.