Algebraisch abgeschlossen
- Algebraisch abgeschlossen
-
In der abstrakten Algebra heißt ein Körper K algebraisch abgeschlossen, wenn jedes nicht konstante Polynom in einer Variablen mit Koeffizienten in K eine Nullstelle in K hat. Folgende Eigenschaften sind äquivalent:
- K ist algebraisch abgeschlossen
- jedes Polynom
![f\in K[X]\setminus K](/pictures/dewiki/53/502a39e29bb7efb08cedd15afe3c4e01.png) zerfällt über K in Linearfaktoren
zerfällt über K in Linearfaktoren
- die irreduziblen Polynome in K[X] sind genau diejenigen vom Grad 1
- für jede algebraische Erweiterung L / K gilt L = K
- für jede natürliche Zahl n hat jeder Endomorphismus von Kn einen Eigenvektor
Beispielsweise ist der Körper der reellen Zahlen nicht algebraisch abgeschlossen, denn das Polynom X2 + 1 hat in  keine Nullstelle. Der Körper
keine Nullstelle. Der Körper  der komplexen Zahlen dagegen ist algebraisch abgeschlossen; diese Aussage bildet den Fundamentalsatz der Algebra. Der Körper der algebraischen Zahlen über
der komplexen Zahlen dagegen ist algebraisch abgeschlossen; diese Aussage bildet den Fundamentalsatz der Algebra. Der Körper der algebraischen Zahlen über  ist trivialerweise algebraisch abgeschlossen. Es gibt keinen endlichen algebraisch abgeschlossenen Körper, denn ist
ist trivialerweise algebraisch abgeschlossen. Es gibt keinen endlichen algebraisch abgeschlossenen Körper, denn ist 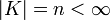 , so ist Xn − X + 1 mit dem Satz von Lagrange identisch 1 und hat somit keine Nullstelle in K.
, so ist Xn − X + 1 mit dem Satz von Lagrange identisch 1 und hat somit keine Nullstelle in K.
Ist ein Körper nicht algebraisch abgeschlossen, dann kann man ihm formal die Nullstellen von Polynomen über diesem Körper hinzufügen, und unter Verwendung des Lemmas von Zorn einen algebraischen Abschluss dieses Körpers konstruieren.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
algebraisch abgeschlossen — algebraisch abgeschlossen, Eigenschaft eines Körpers K, wenn jede algebraische Gleichung mit Koeffizienten aus K eine Lösung besitzt, die selbst Element aus K ist. Jedes algebraische Element über einen algebraisch abgeschlossenen Körper K… … Universal-Lexikon
Algebraisch — Statue Al Chwarizmis, Al Khwarizmi, Technische Universität Teheran Die Algebra ist eines der grundlegenden Teilgebiete der Mathematik, das sich der Struktur, Relation und der Menge widmet. Im Volksmund wird Algebra häufig als das Rechnen mit… … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Fehlstand — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Integrabel — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Kollinear — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Kopunktal — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Mathematisches Attribut — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Multivariat — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
![f\in K[X]\setminus K](/pictures/dewiki/53/502a39e29bb7efb08cedd15afe3c4e01.png) zerfällt über K in Linearfaktoren
zerfällt über K in Linearfaktoren keine Nullstelle. Der Körper
keine Nullstelle. Der Körper  der komplexen Zahlen dagegen ist algebraisch abgeschlossen; diese Aussage bildet den Fundamentalsatz der Algebra. Der Körper der algebraischen Zahlen über
der komplexen Zahlen dagegen ist algebraisch abgeschlossen; diese Aussage bildet den Fundamentalsatz der Algebra. Der Körper der algebraischen Zahlen über  ist trivialerweise algebraisch abgeschlossen. Es gibt keinen endlichen algebraisch abgeschlossenen Körper, denn ist
ist trivialerweise algebraisch abgeschlossen. Es gibt keinen endlichen algebraisch abgeschlossenen Körper, denn ist 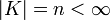 , so ist Xn − X + 1 mit dem Satz von Lagrange identisch 1 und hat somit keine Nullstelle in K.
, so ist Xn − X + 1 mit dem Satz von Lagrange identisch 1 und hat somit keine Nullstelle in K.