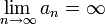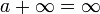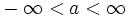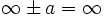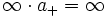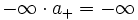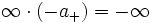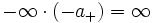- Unendlich
-
Der Begriff Unendlichkeit bezeichnet die Negation bzw. Aufhebung von Endlichkeit, weniger präzise auch deren "Gegenteil". Sein mathematisches Symbol ist ∞. Das Unendliche - im Sinne von: das Nichtendliche - ist der direkten menschlichen Erfahrung unzugänglich und am ehesten mit dem Begriff der unbegrenzten Weite zu assoziieren.
Inhaltsverzeichnis
Wissenschaftliche Zugänge zum Begriff „Unendlichkeit“
Die Unendlichkeit lässt sich geistes- oder naturwissenschaftlich nur abstrakt in der Vorstellung entwickeln und wird auf Objekte und Begriffe angewendet, die keine räumlichen oder zeitlichen Grenzen haben. In der Theologie und manchen philosophischen Konzeptionen ist die Unendlichkeit eines der Attribute Gottes, während die Schöpfung per se endlich ist.
In der Philosophie existieren seit Aristoteles zwei Auffassungen vom Begriff des Unendlichen: das aktual Unendliche und das potentiell Unendliche. Leonardo da Vinci symbolisierte die Unendlichkeit mit der Unendlichkeitsmaschine.
In der Astronomie wurde angesichts der Tiefe und Weite des Sternhimmels oft die Vorstellung eines unendlich ausgedehnten Weltraums entwickelt. Auch in Bezug auf die Zeit ist das Konzept der Unendlichkeit bekannt, hier verwendet man den Begriff Ewigkeit. Während die Höhere Mathematik oft mit dem Abstraktum „unendlich“ operiert, ist in der theoretischen Physik eher das Phänomen der Singularität von Bedeutung – etwa im Zusammenhang mit den Begriffen Urknall (Beginn des sichtbaren Universums) und Schwarzes Loch. Als Singularität wird ein Punkt in der Raumzeit bezeichnet, an dem Masse in einem ausdehnungslosen Punkt mit unendlicher Dichte konzentriert ist.
In der Mathematik und Physik werden unendliche Werte durch das Symbol
 dargestellt, das der Lemniskate genannten algebraischen Kurve vierten Grades gleicht (eine auf der Seite liegende 8). Das Symbol wurde vom englischen Mathematiker John Wallis 1655 als Zeichen für eine abstrakte unendliche Größe eingeführt. Ursprünglich wurde
dargestellt, das der Lemniskate genannten algebraischen Kurve vierten Grades gleicht (eine auf der Seite liegende 8). Das Symbol wurde vom englischen Mathematiker John Wallis 1655 als Zeichen für eine abstrakte unendliche Größe eingeführt. Ursprünglich wurde  im alten Rom als Zeichen für die Zahl 1000 verwendet. Anderen Deutungen zufolge entstand es aus dem letzten griechischen Buchstaben ω (kleines Omega) – einem gebräuchlichen Synonym für „Ende“ – oder dem kleinen liegenden θ (Theta), dem Anfangsbuchstaben für Gott (theos).
im alten Rom als Zeichen für die Zahl 1000 verwendet. Anderen Deutungen zufolge entstand es aus dem letzten griechischen Buchstaben ω (kleines Omega) – einem gebräuchlichen Synonym für „Ende“ – oder dem kleinen liegenden θ (Theta), dem Anfangsbuchstaben für Gott (theos).Neben der unendlichen Ausdehnung zu immer weiter zunehmenden Größen wird der Begriff auch für die unendliche Teilbarkeit, das unendlich Feine verwendet, dessen Grenze null ist, null aber nicht erreicht. Aus der Negation des unendlich Feinen und deren Paradoxien ergab sich die ursprüngliche griechische „Atomtheorie“ des „Unteilbaren“.
Unendlichkeit in der Mathematik
Die Mathematik kennt den Begriff „Unendlich“ in verschiedenen Teildisziplinen. Diese unterschiedlichen „Unendlichkeiten“ haben jeweils ihre eigenen Eigenschaften, und die Unendlichkeitbegriffe sind nicht austauschbar. Die Begriffe sind manchmal sehr unanschaulich und bereiten Nichtmathematikern deshalb Schwierigkeiten. Es kann helfen, wenn man sich klar macht, dass die Mathematik in der Regel keine Aussagen darüber macht, was Unendlichkeit „in Wirklichkeit“ ist. Stattdessen werden Regeln für die Manipulation von Symbolen aufgestellt.
Siehe auch: endliche und unendliche Menge.
Analysis
Das Symbol
 wird in der Analysis verwendet, um anzuzeigen, dass eine Folge reeller Zahlen oder eine andere reellwertige Funktion über alle Grenzen wächst. Die Aussage
wird in der Analysis verwendet, um anzuzeigen, dass eine Folge reeller Zahlen oder eine andere reellwertige Funktion über alle Grenzen wächst. Die Aussagebedeutet allerdings nicht, dass die Folge konvergiert, denn das Symbol
 , das hier als Grenzwert der Folge (an) bezeichnet wird, ist keine reelle Zahl.
, das hier als Grenzwert der Folge (an) bezeichnet wird, ist keine reelle Zahl.- Siehe auch: Grenzwert (Folge), Grenzwert (Funktion)
Rechenregeln für
 sind also stets als Aussagen über (uneigentliche) Grenzwerte zu betrachten. So bedeutet die Rechenregel
sind also stets als Aussagen über (uneigentliche) Grenzwerte zu betrachten. So bedeutet die Rechenregelnur Folgendes:
- „Sind (an) und (bn) zwei Folgen reeller Zahlen, so dass (an) gegen a konvergiert und (bn) über alle Grenzen wächst, dann gilt für die Folge (an + bn), dass sie über alle Grenzen wächst.“
Dies ist für jede reelle Zahl a richtig.
Wäre dagegen „
 “ eine reelle Zahl, so würde aus der oben genannten Rechenregel eine Gleichung, bei der man „
“ eine reelle Zahl, so würde aus der oben genannten Rechenregel eine Gleichung, bei der man „ “ auf beiden Seiten subtrahieren könnte, was a = 0 ergibt, also keineswegs für jede reelle Zahl a richtig ist.
“ auf beiden Seiten subtrahieren könnte, was a = 0 ergibt, also keineswegs für jede reelle Zahl a richtig ist.Hinweis:
Für viele Zwecke in der (reellen) Analysis ist es angebracht, zwischen
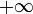 und
und 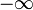 zu unterscheiden. Dieser Zweig der Mathematik benutzt also zwei unendliche Elemente.
zu unterscheiden. Dieser Zweig der Mathematik benutzt also zwei unendliche Elemente.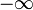 bedeutet dann, dass ein Grenzwert kleiner ist als jede reelle Zahl. In diesem Sinne gilt z. B. für jede reelle Zahl a
bedeutet dann, dass ein Grenzwert kleiner ist als jede reelle Zahl. In diesem Sinne gilt z. B. für jede reelle Zahl a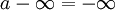 .
.
Weitere Operationen mit

Auch die folgenden Regeln sind zu lesen als Aussagen über Folgen, die entweder a oder
 als Grenzwert haben. Dass sie mit einem Gleichheitszeichen geschrieben werden, erlaubt nicht, sie wie Gleichungen zu behandeln. a steht für eine beliebige reelle Zahl.
als Grenzwert haben. Dass sie mit einem Gleichheitszeichen geschrieben werden, erlaubt nicht, sie wie Gleichungen zu behandeln. a steht für eine beliebige reelle Zahl. liegt „jenseits“ der Zahlengeraden:
liegt „jenseits“ der Zahlengeraden:
 ändert sich nicht, wenn man eine endliche Zahl addiert oder subtrahiert:
ändert sich nicht, wenn man eine endliche Zahl addiert oder subtrahiert:
- Auch wenn
 hinzugefügt wird, ändert sich nichts:
hinzugefügt wird, ändert sich nichts:
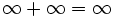 und
und 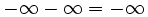
- Falls zwei Unendlichkeiten von einander subtrahiert werden so ist das Ergebnis nicht definiert:
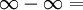 undefiniert
undefiniert
- Bei der Multiplikation und der Division sind die Vorzeichenregeln zu beachten:
- „a + “ steht hier für eine beliebige positive reelle Zahl.
- Bei der Multiplikation dürfen wie üblich die Faktoren vertauscht werden, also
 usw.
usw.
- Bei der Division gilt
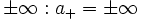 usw., aber:
usw., aber:
- Eine Zahl geteilt durch Unendlich ergibt null:
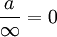 und
und 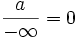
- Es sei darauf hingewiesen, dass dies nicht in die Gleichung
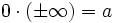 umgewandelt werden kann!
umgewandelt werden kann!
Undefinierte Operationen
Ist nämlich (an) eine Folge mit dem Grenzwert 0 und (bn) eine Folge mit dem Grenzwert
 , so kann die Folge
, so kann die Folge 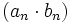 jede reelle Zahl (einschließlich 0) als Grenzwert haben oder gegen
jede reelle Zahl (einschließlich 0) als Grenzwert haben oder gegen  oder gegen
oder gegen 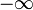 streben, oder auch gar keinen Grenzwert haben, je nachdem, wie die Folgen (an) und (bn) beschaffen sind.
streben, oder auch gar keinen Grenzwert haben, je nachdem, wie die Folgen (an) und (bn) beschaffen sind.Zum Beispiel ergibt sich:
- für
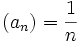 und (bn) = n:
und (bn) = n: 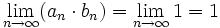
- für
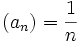 und (bn) = n2:
und (bn) = n2: 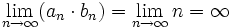 und
und - für
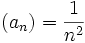 und (bn) = n:
und (bn) = n: 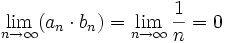
Der Ausdruck
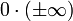 ist also undefiniert; er bezeichnet weder eine reelle Zahl, noch kann ihm das Symbol
ist also undefiniert; er bezeichnet weder eine reelle Zahl, noch kann ihm das Symbol  zugeordnet werden.
zugeordnet werden.Weitere undefinierte Ausdrücke sind:
 ; beschränkt man sich allerdings auf Folgen von positiven reellen Zahlen, so gilt
; beschränkt man sich allerdings auf Folgen von positiven reellen Zahlen, so gilt 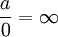 .
.
Nichtstandardanalysis
In der Nichtstandardanalysis wird mit hyperreellen Zahlen gerechnet, bei denen es auch unendliche Zahlen gibt. Dabei gelten die bekannten Rechenregeln.
Topologie
Mit Methoden der Topologie ist es möglich, den Grenzwertbegriff so zu fassen, dass der umgangssprachliche Sinn von „Unendlichkeit“ vollständig eliminiert wird.
Dazu wird die Menge
 erweitert zu einer Menge
erweitert zu einer Menge  . Auf
. Auf  lässt sich eine Topologie so definieren, dass Funktionen, die in
lässt sich eine Topologie so definieren, dass Funktionen, die in  gegen Unendlich streben, in
gegen Unendlich streben, in  eine stetige Fortsetzung haben.
eine stetige Fortsetzung haben.Funktionentheorie
In der Theorie der komplexwertigen Funktionen einer komplexen Variablen (Funktionentheorie) erweist es sich, anders als bei den reellen Zahlen, als günstig, nur einen mit ∞ bezeichneten Grenzwert zu verwenden. Es wird festgesetzt:
Wächst in der komplexen Zahlenebene bei einer Zahlenfolge (z. B. bei gleich bleibendem Argument) der Betrag über alle Grenzen, so wird als Grenzwert einer solchen Folge stets das gleiche Element ∞ verwendet.
Die komplexe Zahlenebene schließt sich damit zu einer Kugel (Riemannsche Zahlenkugel). „∞“ ist der Gegenpol zur Zahl Null.
Hinweis: Auch in anderen Zusammenhängen ist es praktisch, nur einen unendlichen Wert zu verwenden. So ist z. B. die Steigung einer Geraden entweder eine reelle Zahl oder „Unendlich“. (Ein Vorzeichen ergäbe hierbei keinen Sinn).
Projektive Geometrie
Bei der Erweiterung einer affinen Ebene zu einer projektiven Ebene werden „unendlich ferne Punkte“ (Fernpunkte) hinzugefügt, die als Schnittpunkte der (bis dahin) parallelen Geraden dienen. („Parallelen schneiden sich im Unendlichen.“) Für jede Richtung, die Geraden haben können, wird genau ein neuer Punkt definiert. Die Gesamtheit dieser „unendlich fernen“ Punkte heißt die „unendlich ferne Gerade“.
Bei diesem Vorgehen entstehen genau so viele unendliche Objekte, wie eine Gerade Punkte hat (zuzüglich einem, nämlich der unendlich fernen Geraden). Je nachdem, von welcher affinen Ebene ausgegangen wird, kann diese Anzahl endlich oder unendlich sein. Ausgehend von der üblichen euklidischen Ebene
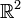 ergeben sich so viele „unendlich ferne Punkte“, wie es reelle Zahlen gibt.
ergeben sich so viele „unendlich ferne Punkte“, wie es reelle Zahlen gibt.Auch hier dient der Begriff „unendlich“ nur dazu, die formale Definition zu motivieren. Werden projektive Ebenen ohne Bezug auf eine affine Ebene betrachtet, so spielt dieser Begriff keine Rolle.
Andererseits ist die Begriffsbildung auch sehr anschaulich: In der Perspektivenkonstruktion sieht man, dass alle Geraden, die „in Wirklichkeit“ dieselbe Richtung haben, sich im perspektivischen Bild im selben Fluchtpunkt schneiden.
Mengenlehre
Kardinalzahlen
In der Mengenlehre wird die Größe von Mengen, auch Mächtigkeit genannt, durch so genannte Kardinalzahlen beschrieben. Bei endlichen Mengen lässt sich die Mächtigkeit z. B. der Menge {A, B, C} durch die Kardinalzahlen 3 angeben: Die Menge {A, B, C} hat drei Elemente. Um die Mächtigkeit unendlicher Mengen zu beschreiben, hat Georg Cantor unendliche Kardinalzahlen eingeführt, die er mit dem hebräischen Buchstaben
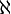 (Aleph) bezeichnet und durchnummeriert:
(Aleph) bezeichnet und durchnummeriert:  ,
, 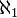 ,
, 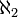 , …
, …- Die Mächtigkeit der Menge der natürlichen Zahlen ist
 , die erste unendliche Kardinalzahl. Mengen mit dieser Mächtigkeit nennt man abzählbar.
, die erste unendliche Kardinalzahl. Mengen mit dieser Mächtigkeit nennt man abzählbar.
- Im ersten Cantorschen Diagonalverfahren zeigt Georg Cantor, dass die Menge der natürlichen Zahlen und die Menge der rationalen Zahlen dieselbe Mächtigkeit
 haben.
haben.
- Im zweiten Cantorschen Diagonalverfahren zeigt Georg Cantor, dass die Menge der reellen Zahlen eine größere Mächtigkeit besitzt als
 : sie ist überabzählbar. Ihre Mächtigkeit ist die der Potenzmenge der natürlichen Zahlen,
: sie ist überabzählbar. Ihre Mächtigkeit ist die der Potenzmenge der natürlichen Zahlen, 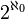 .
.
- Ein im Rahmen der Mengenlehre nicht zu beantwortendes Problem ist die Kontinuumshypothese, ob die Mächtigkeit der reellen Zahlen mit der zweiten unendlichen Kardinalzahl
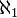 übereinstimmt. (Die Kontinuumshypothese oder ihre Negation kann als neues Axiom in der Mengenlehre verwendet werden.)
übereinstimmt. (Die Kontinuumshypothese oder ihre Negation kann als neues Axiom in der Mengenlehre verwendet werden.)
- Die unendlichen Kardinalzahlen bilden ihrerseits wieder eine unendliche Folge: Da die Potenzmenge einer Menge stets eine größere Mächtigkeit hat als die Menge selbst, gibt es keine größte Kardinalzahl.
Ordinalzahlen
Eine weitere Möglichkeit, die Unendlichkeit zu quantifizieren, bieten die transfiniten Ordinalzahlen: Sie entsprechen einer Anordnung unendlich vieler Objekte. Ihre Arithmetik unterscheidet sich von der der Kardinalzahlen: Beispielsweise haben zwei Kopien der natürlichen Zahlen zusammen immer noch die Mächtigkeit
 , aber die entsprechende Ordinalzahl ω + ω ist größer als die zu den natürlichen Zahlen gehörende Ordinalzahl ω.
, aber die entsprechende Ordinalzahl ω + ω ist größer als die zu den natürlichen Zahlen gehörende Ordinalzahl ω.Literatur
- Amir D. Aczel: Die Natur der Unendlichkeit. Mathematik, Kabbala und das Geheimnis des Aleph. rororo Taschenbücher, 2002 ISBN 3-499-61358-1
- Herbert Beckert: Zur Erkenntnis des Unendlichen. Hirzel, Stuttgart 2001 ISBN 3-7776-1136-0 (Abhandlungen der Sächsischen Akademie der Wissenschaften zu Leipzig)
- Albrecht Beutelspacher: Pasta all’infinito. Meine italienische Reise in die Mathematik. dtv Taschenbücher, 2001 ISBN 3-423-33069-4
- Rudolf Taschner: Das Unendliche. Mathematiker ringen um einen Begriff. Springer Verlag, 1995 ISBN 3-540-59093-5
- Hans Lauwerier: Unendlichkeit. Denken im Grenzenlosen. Rowohlt, 1993.
- Eli Maor: To Infinity and Beyond. A Cultural History of the Infinite. Birkhäuser, Stuttgart 1986.
- Raymond Smullyan: Satan, Cantor und die Unendlichkeit. Insel-Verlag, Frankfurt 1997
- David Hilbert: Über das Unendliche. Mathematische Annalen 95, 161–190, 1926. Digitalisierte Fassung
Weblinks
- E. D. Buckner: Philosophy and Infinity (Sammlung klassischer Texte zum Thema) (engl.)
- Rudolf Eisler: Unendlich, in: Wörterbuch der philosophischen Begriffe, 1904 (mit Unterpunkten)
Wikimedia Foundation.