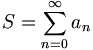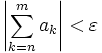Cauchy-Folge — Als Cauchy Folge wird in der Mathematik eine Folge mit einer speziellen Eigenschaft bezeichnet, die eng mit dem Begriff der Konvergenz zusammenhängt. Diese Folgen sind nach dem französischen Mathematiker Augustin Louis Cauchy benannt und von… … Deutsch Wikipedia
Cauchy — ist der Name folgender Personen: Augustin Louis Cauchy (1789–1857), französischer Mathematiker Cauchy ist der Name folgender Ortschaften in Frankreich: Cauchy à la Tour, Gemeinde im Département Pas de Calais Cauchy, ehemaliger Name der Gemeinde… … Deutsch Wikipedia
Cauchy-Filter — Uniforme Räume im Teilgebiet Topologie der Mathematik sind Verallgemeinerungen von metrischen Räumen. Jeder metrische Raum kann auf natürliche Weise als uniformer Raum betrachtet werden, und jeder uniforme Raum kann auf natürliche Weise als… … Deutsch Wikipedia
Cauchyfolge — Als Cauchy Folge wird in der Mathematik eine Folge mit einer speziellen Eigenschaft bezeichnet, die eng mit dem Begriff der Konvergenz zusammenhängt. Diese Folgen sind nach dem französischen Mathematiker Augustin Louis Cauchy benannt und von… … Deutsch Wikipedia
Fundamentale Folge — Als Cauchy Folge wird in der Mathematik eine Folge mit einer speziellen Eigenschaft bezeichnet, die eng mit dem Begriff der Konvergenz zusammenhängt. Diese Folgen sind nach dem französischen Mathematiker Augustin Louis Cauchy benannt und von… … Deutsch Wikipedia
In sich konvergent — Als Cauchy Folge wird in der Mathematik eine Folge mit einer speziellen Eigenschaft bezeichnet, die eng mit dem Begriff der Konvergenz zusammenhängt. Diese Folgen sind nach dem französischen Mathematiker Augustin Louis Cauchy benannt und von… … Deutsch Wikipedia
In sich konvergente Folge — Als Cauchy Folge wird in der Mathematik eine Folge mit einer speziellen Eigenschaft bezeichnet, die eng mit dem Begriff der Konvergenz zusammenhängt. Diese Folgen sind nach dem französischen Mathematiker Augustin Louis Cauchy benannt und von… … Deutsch Wikipedia
Konzentrierte Folge — Als Cauchy Folge wird in der Mathematik eine Folge mit einer speziellen Eigenschaft bezeichnet, die eng mit dem Begriff der Konvergenz zusammenhängt. Diese Folgen sind nach dem französischen Mathematiker Augustin Louis Cauchy benannt und von… … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
 ein Index N existiert, so dass für alle m und n mit m > n > N gilt:
ein Index N existiert, so dass für alle m und n mit m > n > N gilt: (bzw.
(bzw.  ). Ist das Kriterium nicht erfüllt, divergiert sie.
). Ist das Kriterium nicht erfüllt, divergiert sie. und
und  folgt dann die Konvergenz der Reihe.
folgt dann die Konvergenz der Reihe.