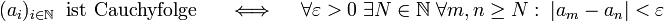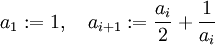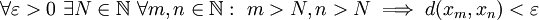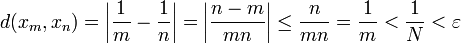Cauchyfolge

Als Cauchy-Folge wird in der Mathematik eine Folge mit einer speziellen Eigenschaft bezeichnet, die eng mit dem Begriff der Konvergenz zusammenhängt. Diese Folgen sind nach dem französischen Mathematiker Augustin Louis Cauchy benannt und von grundlegender Bedeutung für den Aufbau der Analysis.

Cauchy-Folgen werden zuweilen auch als Fundamentalfolgen, konzentrierte Folgen oder in sich konvergente Folgen bezeichnet.

Definition

Eine Folge 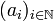$(a_i)_{i\in \mathbb{N}}$ heißt Cauchyfolge, wenn es zu jedem $\varepsilon>0$ einen Index N gibt, so dass ab diesem Index alle Folgenglieder weniger als $\varepsilon$ voneinander entfernt sind.

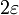Für rationale oder reelle Zahlenfolgen kann man auch sagen, dass es zu jeder noch so kleinen positiven Zahl $\varepsilon$ ein Intervall der Länge $2\varepsilon$ gibt, in dem fast alle Folgenglieder liegen.

In Formeln lautet die oben genannte Definition:

$(a_i)_{i\in \mathbb{N}} \;\text{ ist Cauchyfolge }\quad \iff \quad \forall \varepsilon>0 \; \exists N\in\mathbb{N} \; \forall m,n \ge N: \;\left|a_m-a_n \right|<\varepsilon$

Dies entspricht weitgehend der Definition für konvergente Folgen, jedoch kommt der Grenzwert selbst (also das a in der Definition der Konvergenz) hier nicht vor.

Motivation am Beispiel der rationalen Zahlen

In der Tat gibt es in der Menge $\mathbb{Q}$ der rationalen Zahlen auch Folgen, deren Folgenglieder sich in der beschriebenen Weise „häufen“, ohne einen (rationalen!) Grenzwert zu haben.

Ein Beispiel hierfür ist die Folge, die sich mit der folgenden Bildungsvorschrift ergibt:

$a_1:=1,\quad a_{i+1}:=\frac{a_i}{2} + \frac{1}{a_i}$

Diese Folge 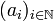$(a_i)_{i\in \mathbb{N}}$ rationaler Zahlen hat als Grenzwert 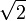$\sqrt{2}$, aber da diese Zahl irrational ist, konvergiert die Folge nicht in $\mathbb{Q}$. Dennoch lässt sich nachweisen, dass die Folge die Cauchy-Eigenschaft besitzt.

Die Problematik, dass in der Menge $\mathbb{Q}$ der rationalen Zahlen viele Grenzwerte von Cauchy-Folgen nicht enthalten sind, führte zu der Idee der Vervollständigung des Zahlenbereichs auf die Menge $\mathbb{R}$ der reellen Zahlen.

Siehe Hauptartikel Vervollständigung

In einem vollständigen Raum konvergiert jede Cauchyfolge, das heißt, in einem solchen Raum besitzt jede Cauchy-Folge einen Grenzwert, der Element des Raumes ist.

Der Begriff der Konvergenz fällt in solchen Räumen mit dem Begriff der Cauchy-Folge zusammen.

Cauchy-Folgen in metrischen Räumen

In der Regel definiert man den Begriff der Cauchy-Folge für eine beliebige Menge X, auf der eine Metrik d gegeben ist. Das Paar (X,d) nennt man dann einen metrischen Raum. Ein Beispiel hierfür ist etwa die Menge der rationalen Zahlen oder der reellen Zahlen mit dem gewöhnlichen Abstand d(x,y) = | x − y | (vgl. oben).

Definition

Sei (X,d) ein metrischer Raum. Eine Folge 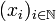$(x_i) _{i\in \mathbb{N}}$ in X heißt Cauchy-Folge, wenn gilt:

$\forall \varepsilon>0 \ \exists N\in\N\ \forall m,n\in\N:\ m>N, n>N\implies d(x_m, x_n) < \varepsilon$

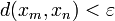Das bedeutet: Zu jedem reellen $\varepsilon > 0$ gibt es eine natürliche Zahl N (Index), so dass für alle natürlichen Zahlen m,n > N gilt: $d(x_m, x_n) < \varepsilon$. Geometrisch verständlicher ist die (äquivalente, aber nicht identische) Formulierung:

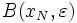Für jeden Radius $\varepsilon > 0$, und sei er noch so klein, gibt es ein Folgenglied x_N (welches einen sehr großen Index N aufweisen kann), so dass alle nachfolgenden Folgenglieder x_n in der offenen Kugel $B(x_N, \varepsilon)$ um den Punkt x_N mit Radius $\varepsilon$ liegen.

Beispiele

Soweit nicht anders erwähnt, beziehen sich die Beispiele auf die reellen Zahlen mit dem gewöhnlichen Abstand.

• Die Folge 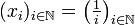$(x_i)_{i\in \mathbb{N}} = \left(\tfrac{1}{i}\right)_{i\in \mathbb{N}}$ ist eine Cauchy-Folge:

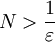Sei $\varepsilon>0$ beliebig vorgegeben. Wähle N so, dass $N>\frac{1}{\varepsilon}$ erfüllt ist. Seien 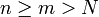$n\geq m>N$ beliebig, dann gilt:

$d(x_m, x_n) = \left|\frac{1}{m} - \frac{1}{n}\right| = \left|\frac{n-m}{mn}\right| \leq \frac{n}{mn} = \frac{1}{m} < \frac{1}{N} < \varepsilon$

• Die Folge 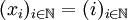$(x_i)_{i\in \mathbb{N}} = (i)_{i\in \mathbb{N}}$ ist keine Cauchy-Folge:

Sei 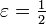$\varepsilon=\tfrac12$ gewählt, und N eine beliebige natürliche Zahl. Dann wähle m = N + 1 und n = m + 1. Es ist dann

$d\left(x_n, x_m\right) = |n-m| = 1 > \varepsilon$,

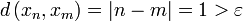die Bedingung einer Cauchy-Folge ist also nicht erfüllt.