Komplexes Netzwerk

Ein komplexes Netzwerk ist im Rahmen der Netzwerkforschung bzw. Graphentheorie ein Netzwerk (Graph) mit nicht-trivialen topologischen Eigenschaften, d. h. mit Eigenschaften, die nicht in einfachen Netzwerken wie Gittern oder zufälligen Graphen auftreten. Die Untersuchung von Komplexen Netzwerken ist ein junges und aktives Gebiet in der aktuellen wissenschaftlichen Forschung, welches hauptsächlich durch die empirischen Untersuchungen von realen Netzwerken wie Computernetzwerken oder sozialen Netzwerken inspiriert ist.

Definition

Zufalls- vs. skalenfreies Netz

Viele soziale, biologische und Computernetzwerke weisen wesentliche nicht-triviale topologische Eigenschaften auf, d. h. die Verbindungen (Kanten) zwischen ihren Elementen (Knoten) sind weder rein regulär noch rein zufällig^[1][2][3][4]. Stattdessen sind derartige Netzwerke durch spezielle Verteilungen im Auftreten ihrer Elemente gekennzeichnet (Grad-Verteilung), durch einen hohen Clusterkoeffizienten, eine bestimmte Gemeinschaftsstruktur (community structure) oder eine ausgeprägte hierarchische Struktur. Viele bisher studierte mathematische Modelle von Netzwerken bzw. Graphen weisen hingegen keine dieser Eigenschaften auf.

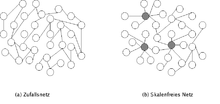
Zwei typische Klassen von komplexen Netzwerken wurden in der Vergangenheit intensiv studiert: Skalenfreie Netzwerke^[5] und die sogenannten small world Netzwerke^[6], deren Entdeckung und Definition kanonische Fallstudien auf diesem Gebiet sind. In skalenfreien Netzwerken haben die Knoten keine typische Anzahl von Verbindungen, sondern die Verteilung der Verbindungen pro Knoten folgt einem Potenzgesetz. In small-world Netzwerken treten hingegen viele sehr kurze Verbindungen zwischen allen Elementen auf und sie haben einen hohen Clusterkoeffizienten. Durch die raschen Fortschritte in der aktuellen Forschung zu komplexen Netzwerken sind auch weitere wichtige neue Aspekte und Erkenntnisse gefunden worden, wie sich zeitliche ändernde Netzwerke: Diese Netzwerke können sich mit der Zeit verändern (sogenannte 'evolving networks'^[7][8]), wobei Knoten und Kanten mit der Zeit neu entstehen oder auch verschwinden können. Dadurch entsteht eine komplexe Dynamik, die zu Selbstorganisation und stabilen Zuständen führen kann. Ein weiterer wichtiger Aspekt ist hier das Auftreten von Synchronisation^[9].

Die Erforschung von komplexen Netzwerken ist ein lebhaftes und sehr aktuelles Forschungsgebiet und verbindet verschiedene Disziplinen, wie Mathematik, Physik, Biologie, Klimaforschung, Informatik, Soziologie, Epidemiologie und viele weitere. Die Konzepte aus der Netzwerktheorie haben Eingang in die Analyse von metabolischen und regulatorischen Netzwerken, in das Design von robusten und skalierbaren Kommunikationsnetzwerken, in die Entwicklung von Impfstrategien oder in die Analyse von Klimaphänomenen gefunden. Entsprechende Forschungsresultate werden regelmäßig in einigen der bekanntesten wissenschaftlichen Zeitschriften veröffentlicht^{[1][6][3][4][10]}, sind Thema auf speziellen Fachtagungen und haben auch zu einigen populärwissenschaftlichen Artikeln und Büchern^[11][12] geführt.

Aus der Erforschung von komplexen Netzwerken können wichtige Aussagen zu Informations- und Stoffflüssen bzw. deren Optimierung sowie über kritisches Verhalten und Stabilität des Gesamtsystems gelernt werden. Als Beispiel sei auf den Austausch von Banknoten hingewiesen, welcher von Dirk Brockmann anhand der Theorie komplexer Netzwerke untersucht wurde, was weltweite Beachtung fand^[10][13].

Literatur

1. ↑ ^{a b} S. H. Strogatz: Exploring Complex Networks. In: Nature. 410, 2001, S. 268-276.
2. ↑ R. Albert, A.-L. Barabási: Statistical mechanics of complex networks. In: Reviews of Modern Physics. 74, 2002, S. 47.
3. ↑ ^{a b} M. E. J. Newman: The structure and function of complex networks. In: SIAM Review. 45, 2003, S. 167-256.
4. ↑ ^{a b} S. Boccaletti et al.: Complex Networks: Structure and Dynamics. In: Physics Reports. 424, 2006, S. 175-308.
5. ↑ A.-L. Barabási, E. Bonabeau: Scale-Free Networks. In: Scientific American. May, 2003, S. 50-59.
6. ↑ ^{a b} D. J. Watts, S. H. Strogatz: Collective dynamics of 'small-world' networks. In: Nature. 393, 1998, S. 440-442.
7. ↑ S. N. Dorogovtsev, J.F.F. Mendes: Evolution of Networks. In: Advances in Physics. 51, 2002, S. 1079.
8. ↑ R. Albert, A.-L. Barabási: Topology of evolving networks: local events and universality. In: Physical Review Letters. 85, 2000, S. 5234-5237.
9. ↑ A. Arenas, A. Díaz-Guilera, J. Kurths, Y. Moreno, C. Zhou: Synchronization in complex networks. In: Physics Reports. 469, 2008, S. 93-153.
10. ↑ ^{a b} Brockmann et al.: The scaling laws of human travel. In: Nature. 439, 2006, S. 462-465.
11. ↑ D. J. Watts: Six Degrees: The Science of a Connected Age. W. W. Norton & Company 2003, ISBN 0-393-04142-5
12. ↑ A.-L. Barabási, Eric Bonabeau: Skalenfreie Netze. In: Spektrum der Wissenschaft. Juli, 2004, S. 62-69.
13. ↑ Money-Circulation Science (Englisch), The New York Times Magazine - The 6th Annual Year in Ideas. Abgerufen am 10. Dezember 2006. 

Siehe auch

• Netzwerke
• Graphentheorie
• Komplexes System
• Selbstorganisation
• Komplexität
• Chaostheorie
• Komplexe Adaptive Systeme
• Nichtlineare Systeme
• System
• Systemeigenschaften