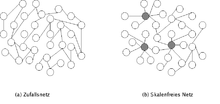
Skalenfreies Netz

Skalenfreie oder Skaleninvariante Netzwerke oder Netze sind komplexe Netzwerke, die keine typische Anzahl von Verbindungen pro Knoten aufweisen. Weil ihr Verlinkungsgrad nicht von der Wahl der Skala abhängt, bezeichnet man sie als skaleninvariant.

Zufalls- vs. skalenfreies Netz

Die Verteilung von Knoten und der Anzahl k von Verbindungen folgt einem Potenzgesetz

$P \propto k^{-\gamma}$

wobei γ eine einheitslose Zahl ist.

Allgemeines

Skalenfreie Netzwerke werden in der Theorie der komplexen Netzwerke untersucht und gelten als relativ ausfallsicher. Die Robustheit solcher Netzwerke besteht allerdings nur bei zufälligen Ausfällen von Knoten. Durch strategisches Vorgehen beim Ausschalten einzelner Knoten (nämlich derjenigen mit hohem Verlinkungsgrad) kann ein skalenfreies Netzwerk schnell in kleine Einzelnetzwerke zerfallen.

Animation: Die Wachstumsstufen nach dem skalenfreien Barabasi–Albert-Modell.

Beispiele für skalenfreie und partiell-skalenfreie Netzwerke sind:

• Netz der Zusammenarbeit von Schauspielern in Filmen (γ = 3), siehe auch Bacon-Zahl
• Stromnetz - z.B. der westlichen USA (γ = 4)
• Der Zitationsgraph (Graph von Zitierungen) von wissenschaftlichen Artikeln (k ist die Zahl der erhaltenen Zitationen, γ = 3)
• Verteilung Einwohnerzahlen von Städten (γ = 2,3), Beispiel siehe Pareto-Verteilung
• Verlinkungsgrad der deutschsprachigen Wikipedia

Viele Kleine-Welt-Netzwerke sind auch skalenfrei bzw. umgekehrt, wobei zu beachten ist, dass normale Zufallsgraphen nicht  skalenfrei sind (Erdös-Rényi- im Gegensatz zu Barabási-Albert-Netzen).

Barabási und Albert schlugen ein vielbeachtetes Modell zur Erzeugung skalenfreier Netzwerke vor. Dabei wird mit einer kleinen Anzahl m₀ von Knoten begonnen und in jedem Schritt ein weiterer Knoten hinzugefügt. Der neue Knoten wird jeweils mit m bereits vorhandenen Knoten verbunden, wobei die Verbindungs-Wahrscheinlichkeit proportional zur Anzahl von Kanten ist, die ein Knoten bereits besitzt. Dieses Prinzip wird auch als preferential attachment bezeichnet. Es lässt sich zeigen, dass in diesem Modell γ gegen den Wert 3 strebt.

Verallgemeinerungen

Viele Netzwerkwahrscheinlichkeiten, z. B. finanzielle Verteilungen, bestehen aus nicht-Gauß'schen Verteilungen mit skalenfreien Ausläuferbereichen (sog. "fat tails"), die das erhöhte Risiko für extreme Gewinne bzw. Verluste(!) quantifizieren, ^[1] , während bei den Gaußverteilungen selbst, mit denen die üblichen Standardbeispiele für Zufallsprozesse formuliert werden, diese extremen Risikobereiche fatalerweise automatisch wegfallen.

Einzelnachweise

1. ↑ R.N. Mantegna, H.E. Stanley, An Introduction to Econophysics. Correlations and Complexity in Finance, Cambridge Univ. Press, Cambridge 1999.

Siehe auch

• Komplexes Netzwerk
• Soziale Netzwerke
• Erdős-Zahl
• neuronales Netz
• Stromnetz

Literatur

• Albert-László Barabási, Eric Bonabeau: Skalenfreie Netze. In: Spektrum der Wissenschaft. Juli 2004, S. 62–69.
• Albert-László Barabási, Réka Albert: Emergence of Scaling in Random Networks. In: Science. Vol. 286, 15, Oktober 1999 (PDF-Datei; 98 kB) doi:10.1126/science.286.5439.509.
• Albert-László Barabási: Linked. How everything is connected to everything else and what it means for business, science, and everyday life. Plume, New York NY 2003, ISBN 0-452-28439-2.
• Paul Erdős, Alfréd Rényi: On the evolution of random graphs. In: Publications of the Mathematical Institute of the Hungarian Academy of Sciences. Vol. 5, 1960, S. 17–61 online (PDF; 5,42 MB).