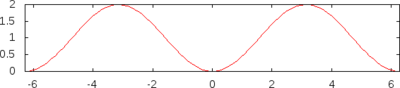
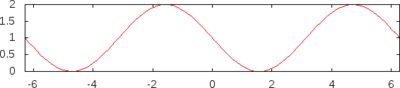
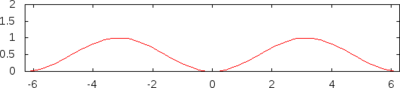
Sinus versus und Kosinus versus

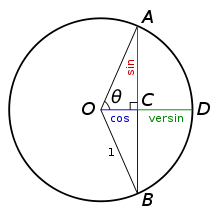
Veranschaulichung am Einheitskreis: Der Sinus versus CD bildet zusammen mit dem Kosinus einen Radius.

Sinus versus (auch Versinus oder Versus, in Formeln abgekürzt $\operatorname{versin}$) und der Kosinus versus (auch Koversinus, in Formeln abgekürzt $\operatorname{coversin}$) sind in der Trigonometrie heute selten verwendete trigonometrische Funktionen. Semiversus (englisch Haversine, in Formeln abgekürzt $\operatorname{sem}$) ist der halbe Sinus versus.

Sinus versus

Versinusfunktion

Definition

Der Sinus Versus wird mit Hilfe der Sinus- oder Kosinusfunktion definiert als^[1]

$\operatorname{versin}(\theta)=1-\cos(\theta)=2\sin^2\left(\frac\theta2\right).$

Der Sinus versus kann auf die ganze komplexe Zahlenebene ausgeweitet werden.

Eigenschaften

Die Ableitung des Sinus Versus ist der Sinus:

$\frac{\mathrm d}{\mathrm dz}\operatorname{versin}(z)=\sin(z).$

Die Stammfunktion ist gegeben durch

$\int\operatorname{versin}(z)\mathrm dz=z-\sin(z)+C.$

Kosinus versus

Koversinusfunktion

Definition

Der Kosinus versus ist der Sinus versus des Gegenarguments:^[2]

$\operatorname{coversin}(\theta)=\operatorname{versin}\left(\frac\pi2-\theta\right)=1-\sin(\theta).$

Semiversus

Semiversusfunktion

Definition

Der Semiversus ist die Hälfte des Sinus versus:^[3]

$\operatorname{sem}(\theta)=\frac{\operatorname{versin}(\theta)}2=\sin^2\left(\frac\theta2\right)$

Geschichte und Verwendung

Der Seiten-Kosinussatz der sphärischen Trigonometrie spielte für die nautische Navigation nach den Sternen in früherer Zeit eine wichtige Rolle^[4]. Um die dabei erforderlichen Multiplikationen trigonometrischer Funktionen durch das Nachschlagen von Tabellenwerten^[5] zu vereinfachen, wurde der Semiversus eingeführt.

Es ergibt sich daraus unter anderem damit der Seiten-Kosinussatz zu:

${\rm sem}(a)={\rm sem}(b-c)+\sin(b) \cdot \sin(c) \cdot {\rm sem}(\alpha)$

Literatur

• M. Abramowitz, I. A. Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, (9)1972, New York: Dover, S. 78

Einzelnachweise

1. ↑ Eric W. Weisstein: Versine. In: MathWorld. (englisch)
2. ↑ Eric W. Weisstein: Coversine. In: MathWorld. (englisch)
3. ↑ Eric W. Weisstein: Haversine. In: MathWorld. (englisch)
4. ↑ Schenk, Bobby: Astronavigation – ohne Formeln – praxisnah. Bielefeld: Verlag Delius Klasing & Co 1978
5. ↑ Fulst, Otto: Nautische Tafeln. Bremen: Geist 1972