Local Outlier Factor

Der Local Outlier Factor (LOF, etwa „Lokaler Ausreißerfaktor“) ist ein Algorithmus zur Erkennung von dichtebasierten Ausreißern von Markus M. Breunig, Hans-Peter Kriegel, Raymond T. Ng und Jörg Sander.^[1] Die Kernidee von LOF besteht darin, die Dichte eines Punktes mit den Dichten seiner Nachbarn zu vergleichen. Ein Punkt, der „dichter“ ist als seine Nachbarn, befindet sich in einem Cluster. Ein Punkt, mit einer deutlich geringeren Dichte als seine Nachbarn, ist hingegen ein Ausreißer.

LOF hat viele Konzepte gemeinsam mit den Clusteranalyse-Algorithmen DBSCAN und OPTICS.

Grundprinzip

Kernidee von LOF: die lokale Dichte eines Punktes mit der seiner Nachbarn vergleichen.

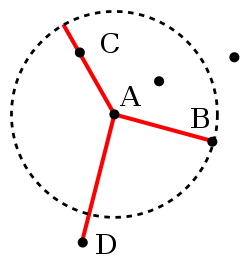
LOF definiert die „lokale Umgebung“ eines Punktes über seine k nächsten Nachbarn. Der Abstand zu diesen wird verwendet, um eine lokale Dichte zu schätzen. In einem zweiten Schritt wird der Quotient aus den lokalen Dichten seiner Nachbarn und der lokalen Dichte des Punktes selbst gebildet. Dieser Wert bewegt sich nahe an 1.0 wenn ein Punkt in einem bereich gleichmäßiger Dichte ist. Für Objekte, die aber abgeschieden von einer solchen Fläche sind, wird der Wert deutlich größer und kennzeichnet so Ausreißer.

Formal

Die k-Distanz(A) ist die Distanz des Objektes A zu seinem k-nächsten Nachbarn. Diese Menge kann gegebenenfalls mehr als k Objekte enthalten, wenn es mehrere Objekte mit dem gleichen Abstand gibt. Wir bezeichnen diese „k-Nachbarschaft“ hier mit N_k(A).

Illustration der Erreichbarkeitsdistanz. Objekte B und C haben die gleiche Erreichbarkeitsdistanz (k=3), während D kein k-nächster Nachbar ist

Basierend auf dieser Distanz wird die „Erreichbarkeitsdistanz“ definiert:

Erreichbarkeitsdistanz_k(A,B) = max{k-Distanz(B),d(A,B)}

Die Erreichbarkeitsdistanz eines Objektes A von B ist also entweder der wahre Abstand, jedoch mindestens die k-Distanz von B. Objekte die zu den k-nächsten Nachbarn von B gehören werden also als gleich weit entfernt betrachtet. Die Motivation für diese Distanzdefinition ist es, stabilere Ergebnisse zu bekommen. (Es handelt sich hierbei aber nicht mehr um eine Distanzfunktion im mathematischen Sinne, da sie nicht symmetrisch ist.)

Die lokale Erreichbarkeitsdichte ("local reachability density", "lrd") eines Objektes A wird definiert als

$\mbox{lrd}(A):=1/\left(\frac{\sum_{B\in N_k(A)}\mbox{Erreichbarkeits-Distanz}_k(A, B)}{|N_k(A)|}\right)$

Diese Dichte ist also der Kehrwert der durchschnittlichen Erreichbarkeitsdistanz des Objektes A von seinen Nachbarn, nicht andersherum die durchschnittliche Erreichbarkeitsdistanz der Nachbarn von A, was definitionsgemäß k-Distanz(A) wäre.

Die lokale Erreichbarkeitsdichte wird jetzt mit denen der Nachbarn verglichen:

$\mbox{LOF}_k(A):=\frac{\sum_{B\in N_k(A)}\frac{\mbox{lrd}(B)}{\mbox{lrd}(A)}}{|N_k(A)|} = \frac{\sum_{B\in N_k(A)}\mbox{lrd}(B)}{|N_k(A)|} / \mbox{lrd}(A)$

Der „Local Outlier Factor“ (LOF) ist also die „Durchschnittliche Erreichbarkeitsdichte der Nachbarn“ dividiert durch die Erreichbarkeitsdichte des Objektes selbst. Ein Wert von etwa 1 bedeutet, dass das Objekt eine mit seinen Nachbarn vergleichbare Dichte hat (also kein Ausreißer ist). Ein Wert kleiner als 1 bedeutet sogar eine dichtere Region (was ein sogenannter „Inlier“ wäre), während signifikant höhere Werte als 1 einen Ausreißer kennzeichnen.

Vorteile

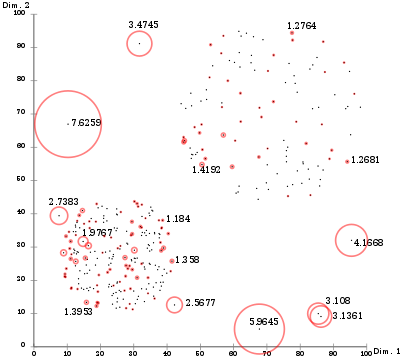LOF-Werte visualisiert mit ELKI. Obwohl der Cluster oben rechts eine mit den Ausreißern unten links vergleichbare Dichte hat, werden sie korrekt klassifiziert.

Im Gegensatz zu vielen globalen Verfahren zur Ausreißererkennung kann LOF mit Bereichen unterschiedlicher Dichte in demselben Datensatz umgehen. Punkte mit einer „mittleren“ Dichte in einer Umgebung mit „hoher“ werden von LOF als Ausreißer klassifiziert, während ein Punkt mit „mittlerer“ Dichte in einer „dünnen“ Umgebung explizit nicht als solcher erkannt wird.

Während die geometrische Intuition von LOF nur in niedrigdimensionalen Vektorräumen Sinn ergibt, kann das Verfahren auf beliebigen Daten angewendet werden, auf denen eine „Unähnlichkeit“ definiert werden kann. Es muss sich dabei nicht um eine Distanzfunktion im strengeren mathematischen Sinne handeln, die Dreiecksungleichung wird beispielsweise nicht benötigt. Der Algorithmus wurde erfolgreich auf verschiedensten Datensätzen eingesetzt, beispielsweise zum Erkennen von Angriffen in Computernetzwerken, wo er bessere Erkennungsraten lieferte als die Vergleichsverfahren.^[2]

Nachteile

Ein wichtiger Nachteil von LOF ist, dass die Ergebniswerte schwer zu interpretieren sind. Werte um 1 und weniger sind sicher keine Ausreißer, aber es gibt keine klare Regel, ab welchem Wert ein Punkt ein signifikanter Ausreißer ist. In einem sehr gleichmäßigen Datensatz sind Werte von 1.1 auffällig, in einem Datensatz mit starken Dichteschwankungen kann ein Wert wie 2 noch ein ganz normaler Datenpunkt sein. Im schlimmsten Falle, treten solche Unterschiede sogar in unterschiedlichen Teilen desselben Datensatzes auf.

Erweiterungen

• Feature Bagging for Outlier Detection ^[3] wendet LOF in mehreren Projektionen an und kombiniert die Ergebnisse, um in hochdimensionalen Daten bessere Ergebnisse zu erhalten.
• Local Outlier Probability (LoOP)^[4] ist eine von LOF abgeleitete Methode, die die Dichte statistisch schätzt, um weniger abhängig vom genauen Wert von k zu werden. Zusätzlich wird das Ergebnis statistisch in den Wertebereich [0:1] normalisiert, um besser interpretierbare Werte zu liefern.
• Interpreting and Unifying Outlier Scores ^[5] stellt eine Normalisierung für LOF und andere Verfahren vor, die die Scores statistisch in das Interval [0:1] normalisiert um die Benutzerfreundlichkeit des Ergebnisses zu verbessern.

Verfügbarkeit

Eine Referenzimplementierung ist im Software-Paket ELKI des Lehrstuhls verfügbar, inklusive Implementierungen von Vergleichsverfahren.

Einzelnachweise

1. ↑ M. M. Breunig, Hans-Peter Kriegel, R.T. Ng, J. Sander: LOF: Identifying Density-based Local Outliers. In: ACM SIGMOD Record. Nr. 29, 2000, doi:10.1145/335191.335388 (http://www.dbs.ifi.lmu.de/Publikationen/Papers/LOF.pdf).
2. ↑ Ar Lazarevic, Aysel Ozgur, Levent Ertoz, Jaideep Srivastava, Vipin Kumar: A comparative study of anomaly detection schemes in network intrusion detection. In: Proc. 3rd SIAM International Conference on Data Mining. 2003 (http://www.siam.org/proceedings/datamining/2003/dm03_03LazarevicA.pdf).
3. ↑ A. Lazarevic, V. Kumar: Feature bagging for outlier detection. In: Proc. 11th ACM SIGKDD international conference on Knowledge Discovery in Data Mining. 2005, doi:10.1145/1081870.1081891.
4. ↑ Hans-Peter Kriegel, P. Kröger, E. Schubert, A. Zimek: LoOP: Local Outlier Probabilities. In: Proc. 18th ACM Conference on Information and Knowledge Management (CIKM). 2009, doi:10.1145/1645953.1646195 (http://www.dbs.ifi.lmu.de/Publikationen/Papers/LoOP1649.pdf).
5. ↑ Hans-Peter Kriegel, Peer Kröger, Erich Schubert, Arthur Zimek: Interpreting and Unifying Outlier Scores. In: Proc. 11th SIAM International Conference on Data Mining. 2011 (http://siam.omnibooksonline.com/data/papers/018.pdf).