OPTICS

OPTICS (Ordering Points To Identify the Clustering Structure, etwa ‚Punkte ordnen um die Clusterstruktur zu identifizieren‘) ist ein dichtebasierter Algorithmus zur Clusteranalyse. Er wurde von Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel und Jörg Sander entwickelt.^[1] Das Grundprinzip des Algorithmus entstammt DBSCAN,^[2] jedoch löst der Algorithmus eine wichtige Schwäche des DBSCAN-Algorithmus: im Gegensatz zu diesem kann er Cluster unterschiedlicher Dichte erkennen. Gleichzeitig eliminiert er (weitgehend) den ε-Parameter des DBSCAN-Algorithmus. Hierzu ordnet OPTICS die Punkte des Datensatzes linear so, dass räumlich benachbarte Punkte in dieser Ordnung nahe aufeinander folgen. Gleichzeitig wird die sogenannte „Erreichbarkeitsdistanz“ notiert. Zeichnet man diese Erreichbarkeitsdistanzen in ein Diagramm, so bilden Cluster „Täler“ und können so identifiziert werden.

Kernidee

OPTICS verwendet wie DBSCAN zwei Parameter, minPts und ε. ε spielt hier jedoch die Rolle einer Maximaldistanz und dient vor allem dazu, die Komplexität des Algorithmus zu begrenzen. Setzt man $\varepsilon = \infty$, so ist die Komplexität des Algorithmus O(n²), andernfalls kann sie mit Hilfe von geeigneten räumlichen Indexstrukturen wie dem R*-Baum auf $O(n\cdot\log n)$ reduziert werden.

In DBSCAN ist ein Punkt ein „Kernpunkt“, wenn seine ε-Umgebung mindestens minPts Punkte enthält. Dies wird in OPTICS umgedreht, und die „Kerndistanz“ als der Abstand zum minPts-nächsten Nachbarn definiert. Die „Kerndistanz“ ist also derjenige ε-Wert, ab dem ein Punkt in DBSCAN ein „Kernpunkt“ wäre. Hat ein Punkt in seiner ε-Umgebung keine minPts Nachbarn, so ist seine Kerndistanz unendlich oder „undefiniert“.

Die „Erreichbarkeitsdistanz“ eines Punktes p von einem zweiten Punkt o ist definiert als max(kerndistanz(o),dist(o,p)), also als das Maximum des echten Abstandes und der Kerndistanz des verweisenden Punktes. Auch hier gilt, dass in DBSCAN diese Distanz dazu führen würde, dass die beiden Objekte im selben Cluster liegen.

OPTICS ordnet jetzt die Objekte in der Datenbank, indem er bei einem beliebigen unbearbeiteten Punkt anfängt, die Nachbarn der ε-Umgebung ermittelt, und sich nach ihrer bisher besten Erreichbarkeitsdistanz in einer Vorrangwarteschlange merkt. Es wird jetzt immer derjenige Punkt als nächstes in die Ordnung aufgenommen, der die kleinste Erreichbarkeitsdistanz hat. Durch das Verarbeiten eines neuen Punktes können sich die Erreichbarkeitsdistanzen der unverarbeiteten Punkte verbessern. Durch die Sortierung dieser Vorrangwarteschlange sucht OPTICS die Mitte eines Clusters und verarbeitet diesen vollständig, bevor er beim nächsten Cluster weitermacht.

Visualisierung

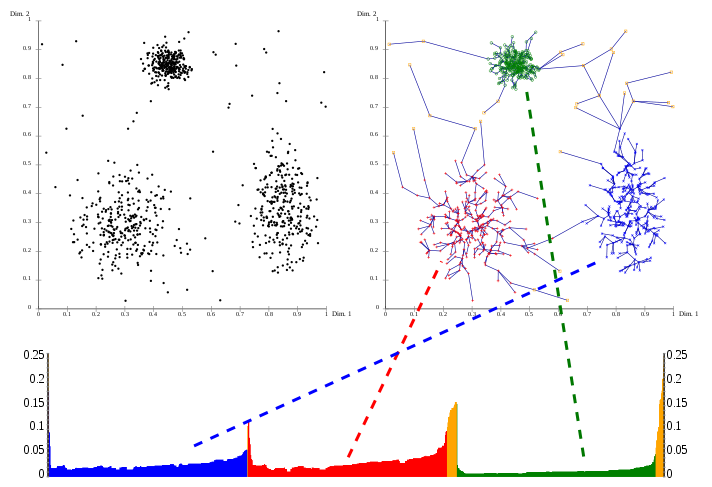
OPTICS kann als Erreichbarkeistdiagramm (unten) visualisiert werden. Hierbei wird an der y-Achse die Erreichbarkeitsdistanz angetragen, die Punkte entlang der x-Achse nach der von OPTICS berechneten Ordnung sortiert. „Täler“ in diesem Diagramm entsprechen erkannten Clustern im Datensatz, die Tiefe des Tales zeigt die Dichte des Clusters an. Als zusätzliche Visualisierung wird hier (rechts oben) jeder Punkt mit seinem Erreichbarkeits-Vorgänger verbunden. Der so entstehende Spannbaum visualisiert den von OPTICS ermittelte Dichte-Verbundenheit der Punkte im Datensatz. Als Parameter wurden hier $\varepsilon \ge 0.5$ und minPts = 10 verwendet. Diese Visualisierung wurde mit der OPTICS-Implementierung in ELKI erstellt.

Pseudocode

Der Grundansatz von OPTICS ist ähnlich zu dem von DBSCAN, aber statt eine Menge von „bekannten aber noch nicht verarbeiteten“ Objekten zu pflegen, werden diese in einer Vorrangwarteschlange (beispielsweise einem indizierten Heap) verwaltet.

 OPTICS(DB, eps, MinPts)
    for each point p of DB
       p.reachability-distance = UNDEFINED
    for each unprocessed point p of DB
       N = getNeighbors(p, eps)
       mark p as processed
       output p to the ordered list
       Seeds = empty priority queue
       if (core-distance(p, eps, Minpts) != UNDEFINED)
          update(N, p, Seeds, eps, Minpts)
          for each next q in Seeds
             N' = getNeighbors(q, eps)
             mark q as processed
             output q to the ordered list
             if (core-distance(q, eps, Minpts) != UNDEFINED)
                update(N', q, Seeds, eps, Minpts)

In update() wird die Vorrangwarteschlange mit der ε-Umgebung von p bzw. q aktualisiert:

 update(N, p, Seeds, eps, Minpts)
    coredist = core-distance(p, eps, MinPts)
    for each o in N
       if (o is not processed)
          new-reach-dist = max(coredist, dist(p,o))
          if (o.reachability-distance == UNDEFINED) // o is not in Seeds
              o.reachability-distance = new-reach-dist
              Seeds.insert(o, new-reach-dist)
          else               // o in Seeds, check for improvement
              if (new-reach-dist < o.reachability-distance)
                 o.reachability-distance = new-reach-dist
                 Seeds.move-up(o, new-reach-dist)

OPTICS gibt die Punkte also in einer bestimmten Reihenfolge aus, annotiert mit ihrer kleinsten Erreichbarkeitsdistanz (der veröffentlichte Algorithmus speichert auch die Kerndistanz, sie wird aber nicht weiter benötigt).

Erweiterungen

OPTICS-OF^[3] ist ein auf OPTICS aufbauendes Verfahren zur Ausreißer-Erkennung. Ein wichtiger Vorteil ist hier, das Cluster im Zuge eines normalen OPTICS-Laufes ermittelt werden können, ohne eine separate Ausreißer-Erkennung durchführen zu müssen.

DeLiClu,^[4] Density-Link-Clustering kombiniert Ideen von Single-Linkage Clustering und OPTICS, eliminiert so den ε-Parameter und erzielt eine verbesserte Performanz gegenüber OPTICS durch Verwendung eines R-Baumes als Index.

HiSC^[5] ist ein hierarchisches (achsen-paralleles) Unterraum-Clustering-Verfahren.

HiCO^[6] ist ein hierarchisches Clustering-Verfahren für beliebig orientierte Unterräume.

DiSH^[7] ist eine Verbesserung von HiSC für komplexere Hierarchien (mit Schnitten von Unterräumen).

Verfügbarkeit

Eine Referenzimplementierung ist im Software-Paket ELKI des Lehrstuhls verfügbar, inklusive Implementierungen von DBSCAN und anderen Vergleichsverfahren.

Einzelnachweise

1. ↑ Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel, Jörg Sander: OPTICS: Ordering Points To Identify the Clustering Structure. In: ACM SIGMOD international conference on Management of data. ACM Press, 1999, S. 49–60 (CiteSeerX).
2. ↑ Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu: A density-based algorithm for discovering clusters in large spatial databases with noise. In: Evangelos Simoudis, Jiawei Han, Usama M. Fayyad (Hrsg.): Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96). AAAI Press, 1996, ISBN 1-57735-004-9, S. 226–231 (CiteSeerX).
3. ↑ Markus M. Breunig, Hans-Peter Kriegel, Raymond T. Ng and Jörg Sander: Principles of Data Mining and Knowledge Discovery. Springer, 1999, ISBN 978-3-540-66490-1, OPTICS-OF: Identifying Local Outliers, S. 262-270, doi:10.1007/b72280 (http://springerlink.metapress.com/content/76bx6413gqb4tvta/).
4. ↑ E. Achtert, C. Böhm, P. Kröger: DeLi-Clu: Boosting Robustness, Completeness, Usability, and Efficiency of Hierarchical Clustering by a Closest Pair Ranking. 2006, S. 119, doi:10.1007/11731139_16.
5. ↑ E. Achtert, C. Böhm, Hans-Peter Kriegel, P. Kröger, I. Müller-Gorman, A. Zimek: Finding Hierarchies of Subspace Clusters. 2006, S. 446, doi:10.1007/11871637_42.
6. ↑ E. Achtert, C. Böhm, P. Kröger, A. Zimek: Mining Hierarchies of Correlation Clusters. 2006, S. 119, doi:10.1109/SSDBM.2006.35.
7. ↑ E. Achtert, C. Böhm, Hans-Peter Kriegel, P. Kröger, I. Müller-Gorman, A. Zimek: Detection and Visualization of Subspace Cluster Hierarchies. 2007, S. 152, doi:10.1007/978-3-540-71703-4_15.