- DBSCAN
-
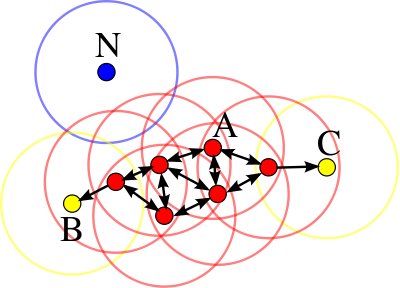
DBSCAN (Density-Based Spatial Clustering of Applications with Noise, etwa: Dichtebasierte räumliche Clusteranalyse mit Rauschen) ist ein von Martin Ester, Hans-Peter Kriegel, Jörg Sander und Xiaowei Xu entwickelter Data-Mining-Algorithmus zur Clusteranalyse. Er ist einer der meist zitierten[1] Algorithmen in diesem Bereich. Der Algorithmus arbeitet dichtebasiert und ist in der Lage, mehrere Cluster zu erkennen. Rauschpunkte werden dabei ignoriert und separat zurückgeliefert.
Punkte bei A sind Kernpunkte. Punkte B und C sind dichte-erreichbar von A und dadurch dichte-verbunden und gehören zu dem gleichen Cluster. Punkt N ist weder ein Kernpunkt, noch dichte-erreichbar, also Rauschen. (MinPts=3 oder MinPts=4)
Die Grundidee des Algorithmus ist der Begriff der „Dichteverbundenheit“. Zwei Objekte gelten als dichte-verbunden, wenn es eine Kette von dichten Objekten („Kernobjekte“, mit mehr als minPts Nachbarn) gibt, die diese Punkte miteinander verbinden. Die durch dieselben Kernobjekte miteinander verbundenen Objekte bilden einen „Cluster“. Objekte, die nicht Teil eines dichte-verbundenen Clusters sind, werden als „Rauschen“ (Noise) bezeichnet.
In DBSCAN gibt es drei Arten von Punkten:
- Kernobjekte, welche selbst dicht sind.
- Dichte-erreichbare Objekte. Dies sind Objekte, die zwar von einem Kernobjekt des Clusters erreicht werden können, selbst aber nicht dicht sind. Anschaulich bilden diese den Rand eines Clusters.
- Rauschpunkte, die weder dicht, noch dichte-erreichbar sind.
Der Algorithmus verfügt über zwei Parameter: ε und minPts. Dabei definiert ε die Nachbarschaft eines Punktes: Von einem Punkt erreichbar ist ein zweiter Punkt genau dann, wenn sein Abstand kleiner als ε ist. minPts definiert dagegen, wann ein Objekt dicht (d.h. ein Kernobjekt) ist: wenn es mindestens minPts ε-erreichbare Nachbarn hat.
Dichte-erreichbare Punkte können von mehr als einem Cluster dichte-erreichbar sein. Diese Punkte werden von dem Algorithmus nicht-deterministisch einem der möglichen Cluster zugeordnet. Dies impliziert auch, dass Dichteverbundenheit nicht transitiv ist; Dichte-Erreichbarkeit ist nicht symmetrisch.
Inhaltsverzeichnis
Wichtige Eigenschaften
DBSCAN ist exakt in Bezug auf die Definition von dichte-verbunden und Noise. Das bedeutet, zwei dichte-verbundene Objekte sind garantiert im selben Cluster, während Rauschobjekte sicher in Noise sind. Nicht exakt ist der Algorithmus bei nur dichte-erreichbaren Clustern, diese werden nur einem Cluster zugeordnet, nicht allen möglichen.
Im Gegensatz beispielsweise zum K-Means-Algorithmus, muss nicht im vornherein bekannt sein, wie viele Cluster existieren.
Der Algorithmus kann Cluster beliebiger Form (z.B. nicht nur kugelförmige) erkennen.
DBSCAN ist weitgehend deterministisch und reihenfolgeunabhängig: Unabhängig davon, in welcher Reihenfolge Objekte in der Datenbank abgelegt oder verarbeitet werden, entstehen die selben Cluster (mit der Ausnahme der nur dichte-erreichbaren Nicht-Kern-Objekte und der Cluster-Nummerierung).
Der Algorithmus kann mit beliebigen Distanzfunktionen und Ähnlichkeitsmaßen verwendet werden. Im Gegensatz zum K-Means-Algorithmus ist kein geometrischer Raum notwendig, da kein Mittelpunkt berechnet werden muss.
DBSCAN selbst ist von linearer Komplexität. Jedes Objekt wird im Wesentlichen nur ein mal besucht. Jedoch ist die Berechnung der ε-Nachbarschaft im Regelfall nicht in konstanter Zeit möglich (ohne entsprechende Vorberechnungen). Ohne die Verwendung von vorberechneten Daten oder einer geeigneten Indexstruktur ist der Algorithmus also von quadratischer Komplexität.
DBSCAN-Algorithmus
Die Originalfassung von DBSCAN[2] kann durch folgenden Pseudocode beschrieben werden:
DBSCAN(D, eps, MinPts) C = 0 for each unvisited point P in dataset D mark P as visited N = D.regionQuery(P, eps) if sizeof(N) < MinPts mark P as NOISE else C = next cluster expandCluster(P, N, C, eps, MinPts) expandCluster(P, N, C, eps, MinPts) add P to cluster C for each point P' in N if P' is not visited mark P' as visited N' = D.regionQuery(P', eps) if sizeof(N') >= MinPts N = N joined with N' if P' is not yet member of any cluster add P' to cluster CAlternativ könnte DBSCAN auch rekursiv implementiert werden (statt dem „join“ von N erfolgt ein rekursiver Aufruf), dies bietet aber keine nennenswerten Vorteile.
DBSCAN (Rekursive Formulierung)
Die rekursive Implementierung zeigt anschaulicher wie DBSCAN arbeitet. Da die Rekursionstiefe aber sehr hoch werden kann, ist die Mengen-basierte normale Formulierung als Implementierung vorzuziehen.
DBSCAN(D, eps, MinPts) C = 0 for each unvisited point P in dataset D mark P as visited N = getNeighbors(P, eps) if sizeof(N) < MinPts mark P as NOISE else C = next cluster add P to cluster C for P' in N if P' is not yet member of any cluster recursiveExpandCluster(P', C, eps, MinPts) recursiveExpandCluster(P, C, eps, MinPts) add P to cluster C if P is not visited mark P as visited N = getNeighbors(P, eps) if sizeof(N) >= MinPts for P' in N if P' is not yet member of any cluster recursiveExpandCluster(P', C, eps, MinPts)Generalisierter DBSCAN
Die generalisierte Version von DBSCAN, GDBSCAN[3][4] abstrahiert hier von der ε-Nachbarschaft und dem minPts-Dichtekriterium. Diese werden ersetzt durch ein Prädikat „getNeighbors“ und einem Prädikat „isCorePoint“.
GDBSCAN(D, getNeighbors, isCorePoint) C = 0 for each unvisited point P in dataset D mark P as visited N = getNeighbors(P) if isCorePoint(P, N) C = next cluster expandCluster(P, N, C) else mark P as NOISE expandCluster(P, N, C) add P to cluster C for each point P' in N if P' is not visited mark P' as visited N' = getNeighbors(P') if isCorePoint(P', N') N = N joined with N' if P' is not yet member of any cluster add P' to cluster CVerwendet man eine ε-Bereichsanfrage als getNeighbors und den minPts-Test als isCorePoint-Prädikat, so erhält man offensichtlich den ursprünglichen DBSCAN-Algorithmus.
Verwendung von DBSCAN
Der Algorithmus DBSCAN ist enthalten in
- Environment for DeveLoping KDD-Applications Supported by Index-Structures (ELKI)
- Waikato Environment for Knowledge Analysis (jedoch ohne Index-Unterstützung)
Auf diesem Algorithmus basieren unter anderem
- OPTICS - Ordering Points To Identify the Clustering Structure
- Shared-Nearest-Neighbor-Clustering - Finding Clusters of Different Sizes, Shapes, and Densities in Noisy, High Dimensional Data
- PreDeCon - Density Connected Clustering with Local Subspace Preferences
- SubClu - Density connected Subspace Clustering for High Dimensional Data
- 4C - Computing Clusters of Correlation Connected Objects
- ERiC - Exploring Complex Relationships of Correlation Clusters
Einzelnachweise
- ↑ Microsoft Academic Search: Meistzitierte Data-Mining-Artikel. Abgerufen am 10.5 (DBSCAN ist ca. Platz 20-25).
- ↑ Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu: A density-based algorithm for discovering clusters in large spatial databases with noise. In: Evangelos Simoudis, Jiawei Han, Usama M. Fayyad (Hrsg.): Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96). AAAI Press, 1996, ISBN 1-57735-004-9, S. 226–231 (http://www.dbs.ifi.lmu.de/Publikationen/Papers/KDD-96.final.frame.pdf).
- ↑ Jörg Sander, Martin Ester, Hans-Peter Kriegel und Xiaowei Xu: Density-Based Clustering in Spatial Databases: The Algorithm GDBSCAN and Its Applications. In: Data Mining and Knowledge Discovery. 2, Springer, Berlin 1998, doi:10.1023/A:1009745219419.
- ↑ Jörg Sander: Generalized Density-Based Clustering for Spatial Data Mining. Herbert Utz Verlag, München 1998, ISBN 3896754696.
Wikimedia Foundation.
