Marching Squares

Schematische Darstellung des Algorithmus: Die grauen Quadrate sind Datenwerte auf einem Gitter. Rot dargestellt ist die Isolinie für einen Isowert im dunklen Grauwertbereich.

Marching Squares (von englisch „marschierende Quadrate“) ist ein Algorithmus aus der Computergrafik zur Berechnung von Isolinien aus einer Datenquelle. Isolinien sind Linien, die Datenpunkte mit gleichen Werten verbinden.

Einleitung

Einige typische Anwendungen für Marching Squares sind die Visualisierung von Isobaren auf Wetterkarten und Niveaulinien in Höhenfeldern. Der Name des Algorithmus leitet sich von seiner Funktionsweise ab. Der Datensatz wird in quadratische Gitterzellen zerlegt, welche nacheinander abgearbeitet werden. Marching Squares ist verwandt mit dem Marching Cubes-Algorithmus, welcher zum Visualisieren von Isoflächen eingesetzt wird.

Funktionsweise

Nachdem der Isowert festgelegt wurde, für den die Linie berechnet werden soll, müssen die Daten in ein Gitter rasterisiert werden, sofern sich der Datensatz nicht schon auf einem gleichmäßigen Gitter befindet. Der Datensatz kann dann in ein gröberes Gitter unterteilt werden. Die Zellen dieses groben Gitters werden schrittweise durchlaufen.

Für jede Gitterzelle wird überprüft, ob ihre Eckpunkte über oder unter dem Isowert liegen. Es können 16 Fälle auftreten, die sich unter Berücksichtigung von Symmetrien auf die folgenden vier zurückführen lassen:

• Fall 1: alle Ecken größer / kleiner
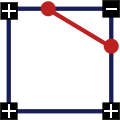
• Fall 2: genau eine Ecke größer / kleiner
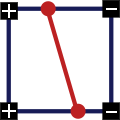
• Fall 3: genau zwei Ecken mit gemeinsamer Kante größer / kleiner
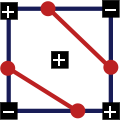
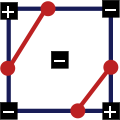
• Fall 4: genau zwei gegenüberliegende Ecken größer / kleiner

Im 4.Fall kann zunächst nicht entschieden werden, wie die beiden Isoliniensegmente durch die Zelle verlaufen müssen. Dafür muss das Innere der Zelle untersucht werden.

• 

  Fall 1: Alle Ecken liegen über (oder unter) dem Isowert.

• 

  Fall 2: Bis auf eine Ecke liegen alle Ecken über (oder unter) dem Isowert.

• 

  Fall 3: Je zwei Ecken an einer Kante liegen über, bzw. unter dem Isowert.

• 

  Fall 4: Je zwei gegenüberliegende Ecken liegen über, bzw. unter dem Isowert.

• 

  Lösung für Fall 4 abhängig von Werten innerhalb der Zelle.

• 

  Lösung für Fall 4 abhängig von Werten innerhalb der Zelle.

Soll die Isolinie feiner abgetastet werden, als es das grobe Gitter zulässt, so kann man in den Fällen 2 bis 4 die Gitterzelle erneut unterteilen und den Algorithmus wiederholt anwenden.

Kanten, bei denen ein Endknoten über dem Isowert und der andere darunter liegt werden von der Isolinie geschnitten. Die Schnittposition kann linear interpoliert werden, da der Isowert I und die Werte f_i an den Endknoten p_i = (x,y) bekannt sind. Für die Berechnung gilt: $I = a \cdot f_1 + b \cdot f_2$ mit a + b = 1

Die Schnittposition ist dann $p_I = a \cdot p_1 + b \cdot p_2$.

veranschaulicht dargestellt

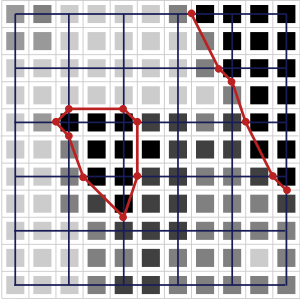
In der englischen Wikipedia ^[1] findet man eine veranschaulichte Version des Marching-Squares-Algorithmus. Hier wird ein Objekt umfahren. Es gibt 16 verschiedene Möglichkeiten. In der Abbildung zeigen die Pfeile in die nächste abzufahrende Richtung.

Quellen

• Kai Hormann: Computergrafik 2. 22.06, abgerufen am 5.09. 
• Stefan Gumhold: Wissenschaftliche Visualisierung. Abbildung. 2009 (Vorlesungsfolien).

Links

• Better know an Algorithm - Marching Square - Eine sehr gute englische Anleitung
• Alle 16 Konfigurationen einer Zelle
• Implementierung in Java

Referenzen

1. ↑ veranschaulichte Version des Marching-Squares-Algorithmus in der englischen Wikipedia