Merkle-Signatur

Die Merkle-Signatur ist ein digitales Signaturverfahren, das auf Merkle-Bäumen sowie Einmalsignaturen wie etwa dem Lamport-Einmalsignaturen basiert. Es wurde von Ralph Merkle in den späten Siebzigern entwickelt und stellt eine Alternative zu traditionellen digitalen Signaturen wie dem Digital Signature Algorithm oder RSA-Kryptosystem dar. Der Vorteil des Signaturverfahrens von Merkle ist, dass es für resistent gegen Angriffe durch Quantencomputer gehalten wird. Die traditionellen Public-Key-Verfahren wie RSA oder Elgamal würden im Falle eines effektiven Quantencomputers unsicher werden (Shor-Algorithmus). Das Merkle-Signaturverfahren hingegen hängt nur von der Existenz sicherer Hashfunktionen ab. Dadurch ist es äußerst anpassbar und resistent gegen Quanten-Computing.

Schlüsselerzeugung

Merkle-Baum mit 8 Blättern

Das Merkle-Signaturverfahren kann nur verwendet werden, um eine begrenzte Anzahl von Nachrichten mit einem öffentlichen Schlüssel pub zu signieren. Die Anzahl möglicher Nachrichten entspricht einer Zweierpotenz und wird daher als N = 2ⁿ bezeichnet.

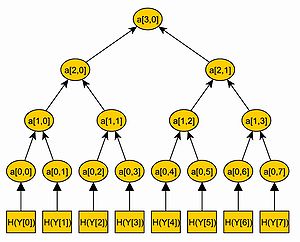
Der erste Schritt bei der Generierung des öffentlichen Schlüssels pub ist die Generierung des öffentlichen Schlüssels X_i und des privaten Schlüssels Y_i von 2ⁿ Einmalsignaturen. Für jeden privaten Schlüssel Y_i mit $1 \leq i \leq 2^n$ wird ein Hash-Wert h_i = H(Y_i) berechnet. Mit diesen Hash-Werten h_i wird ein Hash-Baum aufgebaut.

Ein Knoten des Baums wird mit a_i,j identifiziert, wobei i die Ebene des Knotens bezeichnet. Die Ebene eines Knotens ist über seinen Abstand zu den Blättern definiert. Somit hat ein Blatt die Ebene i = 0 und die Wurzel die Ebene i = n. Die Knoten jeder Ebene sind von links nach rechts durchnummeriert, sodass a_i,0 der Knoten ganz links auf Ebene i ist.

Im Merkle-Baum sind die Hash-Werte h_i die Blätter des Binärbaums, sodass h_i = a_0,i. Jeder innere Knoten des Baums ist der Hash-Wert der Konkatenation seiner beiden Kinder. Beispielsweise ist a_1,0 = H(a_0,0 | | a_0,1) und a_2,0 = H(a_1,0 | | a_1,1).

Auf diese Weise wird ein Baum mit 2ⁿ Blättern und 2^{n + 1} − 1 Knoten aufgebaut. Die Wurzel des Baums a_n,0 ist der öffentliche Schlüssel pub des Merkle-Signaturverfahrens.

Signierung

Merkle-Baum mit Pfad A und Authentifizierungspfad für i=2

Um eine Nachricht M mit dem Merkle-Signaturverfahren zu signieren, wird die Nachricht M zuerst mit einem Einmalsignaturverfahren signiert, wodurch die Signatur sig' entsteht. Dazu wird eines der Schlüsselpaare aus öffentlichem und privatem Schlüssel (X_i,Y_i,) verwendet.

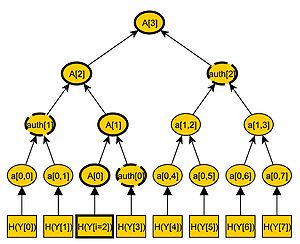
Das einem öffentlichen "einmal" Schlüssel X_i zugehörige Blatt des Hash-Baums ist a_0,i = H(Y_i). Der Pfad im Hash-Baum von a_0,i zur Wurzel wird mit A bezeichnet. Der Pfad A besteht aus n + 1 Knoten, $A_0, \ldots, A_n$, wobei A₀ = a_0,i die Blätter sind und A_n = a_n,0 = pub die Wurzel des Baums ist. Um diesen Pfad A zu berechnen wird jedes Kind der Knoten $A_{1}, \ldots, A_{n}$ benötigt. Es ist bekannt, dass A_i ein Kind von A_{i + 1} ist. Um den nächsten Knoten A_{i + 1} des Pfades A zu berechnen, müssen beide Kinder von A_{i + 1} bekannt sein. Daher wird der Bruder von A_i benötigt. Dieser Knoten wird mit auth_i bezeichnet, sodass A_{i + 1} = H(A_i | | auth_i). Deswegen werden n Knoten $auth_0,\ldots,auth_{n-1}$ benötigt, um jeden Knoten des Pfades A zu berechnen. Diese Knoten $auth_{0}, \ldots , auth_{n-1}$ werden berechnet und gespeichert. Sie bilden zusammen mit einer Einmalsignatur sig' von M die Signatur sig = (sig' | | auth₂ | | auth₃ | | ... | | auth_{n − 1}) des Merkle-Signaturverfahrens.

Verifizierung

Der Empfänger kennt den öffentlichen Schlüssel pub, die Nachricht M, und die Signatur sig = (sig' | | auth₀ | | auth₁ | | ... | | auth_{n − 1}). Zuerst verifiziert der Empfänger die Einmalsignatur sig' der Nachricht M. Falls sig' eine gültige Signatur von M ist, berechnet der Empfänger A₀ = H(Y_i), indem er den Hash-Wert des öffentlichen Schlüssels der Einmalsignatur berechnet. Für j = 1,..,n − 1 werden die Knoten A_j des Pfades A berechnet, mit A_j = H(a_{j − 1} | | b_{j − 1}). Wenn A_n dem öffentlichen Schlüssel pub des Merkle-Signaturverfahrens entspricht, so ist die Signatur gültig.

Quellen

• G. Becker. "Merkle Signature Schemes, Merkle Trees and Their Cryptanalysis", Seminar 'Post Quantum Cryptology' an der Ruhr-Universität Bochum.
• E. Dahmen, M. Dring, E. Klintsevich, J. Buchmann, L.C. Coronado Garca. "CMSS - an improved merkle signature scheme". Progress in Cryptology - Indocrypt 2006, 2006.
• E. Klintsevich, K. Okeya, C.Vuillaume, J. Buchmann, E.Dahmen. "Merkle signatures with virtually unlimited signature capacity". 5th International Conference on Applied Cryptography and Network Security - ACNS07, 2007.
• Ralph Merkle. "Secrecy, authentication and public key systems / A certified digital signature". Ph.D. dissertation, Dept. of Electrical Engineering, Stanford University, 1979. [1]
• S. Micali, M. Jakobsson, T. Leighton, M. Szydlo. "Fractal merkle tree representation and traversal". RSA-CT 03, 2003

Weblinks

• Efficient Use of Merkle Trees - Erklärung von RSA Security zum ursprünglichen Zwecks von Merkle-Trees: der Handhabung vieler Lamport-Einmalsignaturen.