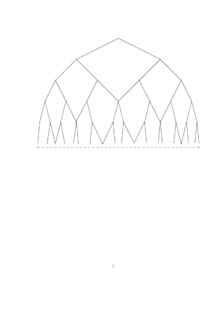
Pisot-Graphen

In der Graphentheorie sind Pisot-Graphen selbstähnliche Graphen die mit Hilfe von Pisot-Zahlen definiert werden.

Definition

Gegeben sei eine Pisot-Zahl α > 1. Auf dem Folgenraum {0,1}ⁿ wird eine Äquivalenzrelation mittels

$s \sim t <=>\sum_{k=0}^{n-1}s_{k}\alpha^{-k}=\sum_{k=0}^{n-1}t_{k}\alpha^{-k}$

definiert.

Die Eckenmenge V des Pisot-Graphen ist durch $V=\bigcup_{n=1}^{\infty} V_{n}$ gegeben, wobei V_n = {0,1}ⁿ / ∼ die Äquivalenzklassen der Relation ∼ bezeichnet. Die Ecke $[s_{1},\dots,s_{n}]$ wird mit $[s_{1},\dots,s_{n},0]$ und $[s_{1},\dots,s_{n},1]$ durch eine Kante verbunden, hierdurch ist die Kantenmenge E gegeben.

Beispiele

Fibonacci-Graph

Der einfachste Pisot-Graph ist der Fibonacci-Graph, er ist durch den goldenenen Schnitt α bestimmt. Er kann auch als Graph der Halbgruppe $\langle G=\ L,R|LRR=RLL\rangle$ beschrieben werden. Weitere Pisot-Graphen erhält man durch andere Pisot-Zahlen. Insbesondere ist der Graph durch x³ + x − 1 = 0 bestimmte Graph nicht planar, siehe Abbildung.

Ein nicht planarer Pisot-Graph

Wachstumsrate

Die Wachstumsrate des Pisot-Graphen ist durch W(α) = log α gegeben. Dies ist eine Konsequenz des klassischen Garsisa-Lemmas. ^[1]

Einzelnachweise

1. ↑ A.M. Garsia, Arithmetic properties of Bernoulli convolutions,Trans. Amer. Math. Soc. 162, 409-432, 1962.

Literatur

• J. Neunhäuserer: Random walks on infinite self-similar graphs. In: Electronic Journal of Probability, Band 12 (2007), Artikel 46, S. 1258-1275.

Weblinks

• Salem Numbers, Pisot Numbers, MahlerMeasure, and Graphs
• J. Neunhäuserer: Random walks on infinite self-similar graphs.