Punkt-in-Polygon-Test nach Jordan

Nach dem Jordanschen Kurvensatz teilen, vereinfacht gesagt, die Ränder eines Polygons den Datenraum in eine Innen- und eine Außenseite. Für viele Anwendungen ist es nötig, herauszufinden, ob ein Punkt innerhalb oder außerhalb eines Polygons liegt.

Strahl-Methode

Beispiel des Tests

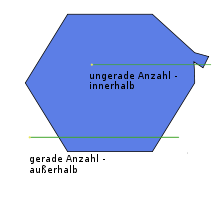
Bei der Strahl-Methode wird von dem zu testenden Punkt ein Strahl in eine beliebige Richtung versendet. Dabei wird gezählt, wie oft der Strahl die Kanten des Polygons schneidet. Es können drei Fälle unterschieden werden:

1. eine gerade Anzahl von Schnittpunkten
2. eine ungerade Anzahl von Schnittpunkten
3. unendlich viele Schnittpunkte

Ist die Anzahl ungerade, liegt der Punkt innerhalb des Polygons, ist sie gerade, liegt er außerhalb. Im Fall von unendlich vielen Schnittpunkten verlief der Strahl direkt auf einer Kante. Der Test muss dann mit einem anderen Winkel wiederholt werden. Durch eine verfeinerter Betrachtung der relativen Lage des Testpunktes und der Kantenenden im kollinearen Fall kann jedoch auf solch eine Wiederholung mit einem anderen Winkel verzichtet werden. So zählt der folgende Pseudocode^[1] entlang dem horizontal nach rechts gerichteten Strahl mit besonderer Beachtung von auf dem Strahl liegenden Ecken:

Funktion:  PunktInPolygon
Parameter: Ecken $P[1],\ldots,P[n]$ eines ebenen Polygons P, Testpunkt Q
Rückgabe:   + 1, wenn Q innerhalb P liegt;  − 1, wenn außerhalb; 0, wenn auf P
  Setze P[0] = P[n] und t =  − 1
  Für $i=0,\ldots,n-1$
    Setze $t = t\cdot$ KreuzProdTest(Q,P[i],P[i + 1])
  Ergebnis: t
  
Funktion:  KreuzProdTest
Parameter: Punkte A = (xA,yA), B = (xB,yB), C = (xC,yC)
Rückgabe:   − 1, wenn der Strahl nach rechts von A die Kante $\overline{BC}$ schneidet (außer im oberen Endpunkt); 0, wenn A auf $\overline{BC}$; sonst  + 1
  Wenn yA = yB = yC
    Wenn $x_B\le x_A \le x_C$ oder $x_C\le x_A\le x_B$
      Ergebnis: 0
    sonst
      Ergebnis:  + 1
  Wenn yB > yC
    Vertausche B und C
  Wenn $y_A\le y_B$ oder yA > yC
    Ergebnis:  + 1
  Setze $\Delta = (x_B-x_A)\cdot(y_C-y_A)-(y_B-y_A)\cdot(x_C-x_A)$
  Wenn Δ > 0
    Ergebnis:  + 1
  sonst wenn Δ < 0
    Ergebnis:  − 1
  sonst
    Ergebnis: 0

Anwendungsgebiete

Diese Methode findet vor allem in Geoinformationssystemen Anwendung.

Literatur

• Günter Hake, Dietmar Grünreich, Liqiu Meng: Kartographie Gruyter, Dezember 2001, 978-3110164046, S. 306ff.
• Norbert Bartelme: Geoinformatik: Modelle, Strukturen, Funktionen, März 2005, 3-540-20254-4, S. 103.

Einzelnachweise

1. ↑ vgl. Jeff Erickson: The Jordan Polygon Theorem. In: Computational Topology. Vorlesungsskript. 2009 (S. 3 – dort fehlt der Fall eines Testpunkts auf einer horizontalen Kante, online, abgerufen am 17. Februar 2011).