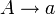Chomskynormalform

Die Chomsky-Normalform (Abk.: CNF) ist eine kontextfreie Grammatik mit einer besonders einfachen Struktur der Produktionen. Sie ist ein Begriff aus der Theorie der formalen Sprachen, einem Teilbereich der Theoretischen Informatik. Sie ist nach dem US-Linguisten Noam Chomsky benannt und kommt beim CYK-Algorithmus zum Einsatz.

Zu jeder kontextfreien Sprache gibt es eine Chomsky-Normalform. Deshalb kann aus jeder kontextfreien Grammatik G eine Chomsky-Normalform G_CNF konstruiert werden, die dieselbe Sprache erzeugt. Die Grammatik G_CNF wird dann auch eine Chomsky-Normalform der kontextfreien Grammatik G genannt.

Eine Erweiterung der Chomsky-Normalform auf kontextsensitive Grammatiken stellt die Kuroda-Normalform dar.

Definition

Eine formale Grammatik ist in Chomsky-Normalform, wenn jede Produktion eine der folgenden Formen hat:

• $A \rightarrow BC$
• $A \rightarrow a$
• $S \rightarrow \epsilon$

wobei A, B und C Nichtterminalsymbole sind und a ein Terminalsymbol ist. S ist das Startsymbol und ε das leere Wort. Wenn die Produktion 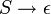$S \rightarrow \epsilon$ zur Grammatik gehört, dann darf S nicht auf der rechten Seite einer Produktion stehen.

Lässt man bei der ersten Produktion auf der rechten Seite beliebig viele anstatt zwei Nichtterminalsymbole zu, so spricht man von einer schwachen Chomsky-Normalform.

Konstruktion einer Chomsky-Normalform

Liegt eine kontextfreie Grammatik vor, so lässt sich daraus schrittweise eine Chomsky-Normalform generieren, die dieselbe Sprache erzeugt:

Eine schwache Chomsky-Normalform erzeugen

Jedem Terminalsymbol a wird ein Nichtterminalsymbol X_a zugeordnet. Auf der rechten Seite jeder Produktion werden sämtliche Terminalsymbole a durch das entsprechende Nichtterminalsymbol X_a ersetzt. Abschließend werden alle Produktionen 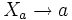$X_a \rightarrow a$ der Grammatik hinzugefügt.

Rechte Seiten mit mehr als zwei Nichtterminalen ersetzen

Sind auf der rechten Seite einer Produktion mehr als zwei Nichtterminale, so werden zwei benachbarte Nichtterminale AB durch ein neues Nichtterminal Y_AB ersetzt. Die Produktion 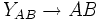$Y_{AB} \rightarrow AB$ wird zur Grammatik hinzugefügt. Dies wiederholt man solange, bis keine Produktion mit mehr als zwei Nichtterminalen mehr vorkommt.

ε-Produktionen entfernen

Streiche die Regeln $A \rightarrow \epsilon$.

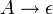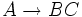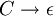Falls Regeln der Art $A \rightarrow BC$ mit $C \rightarrow \epsilon$ existieren, ersetze sie durch $A \rightarrow B$.

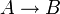Hierbei muss man aufpassen, dass man das Resultat der Abbildungen nicht inhaltlich verändert. Beispiel: eine Abbildung der Startvariable S auf eine oder mehrere Variablen die wiederum auf ε abgebildet werden, sprich die Erzeugung des leeren Wortes, muss auch bei der Grammatik in Chomsky-Normalform möglich sein. S bildet sozusagen eine Ausnahme der obigen Definition, da es die Abbildung 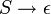$S \rightarrow \epsilon$ geben darf.

Kettenregeln (Produktionen der Form A→B) entfernen

Wenn man eine Kettenregel, d. h. eine Produktion der Form 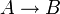$A \rightarrow B$, entfernt, fügt man für jede vorhandene Produktion der Form 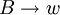$B \rightarrow w$ eine neue Produktion 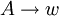$A \rightarrow w$ hinzu, falls diese keine bereits entfernte Kettenregel ergibt. w ist hierbei ein beliebiges Wort aus Nichtterminalen.

Quellen

• Grzegorz Rozenberg, Arto Salomaa: Handbook of Formal Languages. Volume 1. Word, Language, Grammar. Springer-Verlag, 1997, ISBN 3-540-60420-0, S. 124–125

Weblinks

• Programm zur Berechnung von Chomsky-Normalformen (Java-Applet)